Một vật dao động điều hòa trên trục Ox với phương trình x = 4 cos 2 π t − π 3 c m . Thời điểm lần thứ 2014 vật có li độ là x = − 2 c m và đang đi theo chiều dương là
A. 2013,8333 (s)
B. 2013,3333 (s)
C. 2014,3333 (s)
D. 2014,8333 (s)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Trong một chu kỳ thì chỉ có một lần vật đi qua vị trí x = − 2 c m và đang đi theo chiều dương. Xét đến thời điểm đi qua vị trí này lần thứ 2014 thì vật phải quay được 2013 chu kỳ và thêm một góc quay α
Thời gian cần tìm là: Δ t = 2013 T + 5 T 6 = 2013.1 + 5 6 .1 = 2013 , 8333 s

Đáp án A
Trong một chu kỳ thì chỉ có một lần vật đi qua vị trí x = -2 cm và đang đi theo chiều dương. Xét đến thời điểm đi qua vị trí này lần thứ 2014 thì vật phải quay được 2013 chu kỳ và thêm một góc quay . Thời gian cần tìm là:
![]()

Từ pt \(v=16\pi\cos\left(4\pi t-\dfrac{\pi}{6}\right)=16\pi\cos\left(4\pi t-\dfrac{2\pi}{3}+\dfrac{\pi}{2}\right)\) (cm/s), ta suy ra \(\omega=4\pi\left(rad/s\right)\), lại có \(\omega A=16\pi\Leftrightarrow A=\dfrac{16\pi}{\omega}=4\left(cm\right)\)
\(\varphi_0=-\dfrac{2\pi}{3}\); \(T=\dfrac{2\pi}{\omega}=0,5\left(s\right)\)
Đường tròn lượng giác:
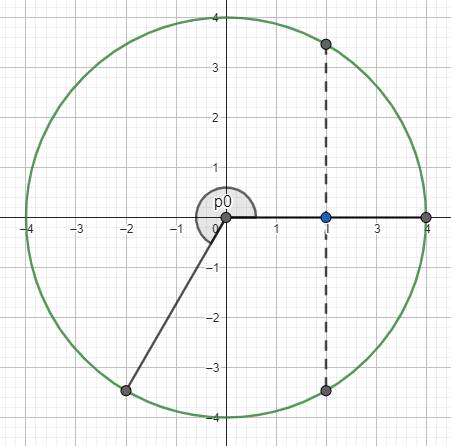
Từ đây, ta có thể thấy tại thời điểm lần thứ 2023 vật chuyển động qua vị trí \(x=2\) kể từ khi dao động, góc quét của vật là \(\Delta\varphi=\dfrac{\pi}{3}+1011.2\pi=\dfrac{6067}{3}\pi\) (rad)
Thời điểm lần thứ 2023 vật chuyển động qua vị trí \(x=2\) kể từ lúc bắt đầu dao động là \(\Delta t=\dfrac{\Delta\varphi}{2\pi}.T=\dfrac{\dfrac{6067}{3}\pi}{2\pi}.0,5=\dfrac{6067}{12}\approx505,58\left(s\right)\)

Chọn A
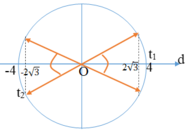
Khoảng cách giữa hai vật theo phương Ox là:
![]()
Theo bài ra ta có d ≥ 2√3
Trong khoảng t1 = 1/24 s đến t2 = 1/3s = t1 + T/2 +T/12, d có độ lớn không nhỏ hơn 2√3 trong khoảng thời gian là:
∆t = T/12 + 2. T/12 = 1/8s.
Chọn đáp án A
Trong một chu kỳ thì chỉ có một lần vật đi qua vị trí x = -2 cm và đang đi theo chiều dương. Xét đến thời điểm đi qua vị trí này lần thứ 2014 thì vật phải quay được 2013 chu kỳ và thêm một góc quay α . Thời gian cần tìm là:
Δ t = 2013 T + 5 T 6 = 2013.1 + 5 6 .1 = 2013 , 8333 s