Tìm m để hàm số
y
=
x
-
3
m
-
x
nghịch biến trên (0;1). ...
Đọc tiếp
Tìm m để hàm số y = x - 3 m - x nghịch biến trên (0;1).
K
Khách
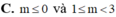
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 2 2022
Bài 1:
a: Để hàm số đồng biến khi x>0 thì m-1>0
hay m>1
b: Để hàm số nghịch biến khi x>0 thì 3-m<0
=>m>3
c: Để hàm số nghịch biến khi x>0 thì m(m-1)<0
hay 0<m<1
19 tháng 2 2022
a, đồng biến khi m - 1 > 0 <=> m > 1
b, nghịch biến khi 3 - m < 0 <=> m > 3
c, nghịch biến khi m^2 - m < 0 <=> m(m-1) < 0
Ta có m - 1 < m
\(\left\{{}\begin{matrix}m-1< 0\\m>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 1\\m>0\end{matrix}\right.\Leftrightarrow0< m< 1\)
29 tháng 9 2016
Theo mình:
để hàm số đồng biến, đk cần là y'=0.
a>0 và \(\Delta'< 0\)
nghịch biến thì a<0
vì denta<0 thì hầm số cùng dấu với a
mình giải được câu a với b
câu c có hai cực trị thì a\(\ne\)0, y'=0, denta>0 (để hàm số có hai nghiệm pb)
câu d dùng viet
câu e mình chưa chắc lắm ^^
22 tháng 11 2023
tròi oi a viết chữ xấu wá đi à, đọc bài của a mà đau mắt wá
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 3 2023
a.
Hàm số nghịch biến khi \(x< 0\Rightarrow-3m-2>0\Rightarrow m< -\dfrac{2}{3}\)
b.
Do \(a=m^2-2m+3=\left(m-1\right)^2+2>0;\forall m\)
\(\Rightarrow\) Hàm đồng biến khi \(x>0\) và nghịch biến khi \(x< 0\)
c.
Hàm đồng biến khi \(x>0\Rightarrow2m+3>0\)
\(\Rightarrow m>-\dfrac{3}{2}\)
26 tháng 12 2021
a, để hàm số nghịch biến thì \(2m+3< 0\Rightarrow m< -\dfrac{3}{2}\)
để hàm số đồng biến thì \(2m+3>0\Rightarrow m>-\dfrac{3}{2}\)
b, Để hàm số y = (2m+3)x-2 song song với đường thẳng y = -5x+3 thì
\(\left\{{}\begin{matrix}2m+3=-5\\-2\ne3\end{matrix}\right.\Rightarrow m=-4\)
KA
30 tháng 10 2021
) Điều kiện để hàm số xác định là m≥0m≥0; x∈Rx∈R
Để hàm số đã cho là hàm bậc nhất thì m√+3√m√+5√≠0m+3m+5≠0
Vì m−−√+3–√≥0+3–√>0m+3≥0+3>0 với mọi m≥0m≥0 nên m−−√+3–√≠0,∀m≥0m+3≠0,∀m≥0
⇒m√+3√m√+5√≠0⇒m+3m+5≠0 với mọi m≥0m≥0
Vậy hàm số là hàm bậc nhất với mọi m≥0m≥0
b)
Để hàm đã cho nghịch biến thì m√+3√m√+5√<0m+3m+5<0
Điều này hoàn toàn vô lý do {m−−√+3–√≥3–√>0m−−√+5–√≥5–√>0{m+3≥3>0m+5≥5>0
Vậy không tồn tại mm để hàm số đã cho nghịch biến trên R
Giải thích các bước giải:
L
1
13 tháng 11 2023
Để hàm số \(y=\dfrac{3-m}{m+3}x-3\) nghịch biến trên R thì \(\dfrac{3-m}{m+3}< 0\)
=>\(\dfrac{m-3}{m+3}>0\)
TH1: \(\left\{{}\begin{matrix}m-3>0\\m+3>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>3\\m>-3\end{matrix}\right.\)
=>m>3
TH2: \(\left\{{}\begin{matrix}m-3< 0\\m+3< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< 3\\m< -3\end{matrix}\right.\)
=>m<-3
11 tháng 11 2023
a: \(y=-x^3-\left(m+1\right)x^2+3\left(m+1\right)x\)
=>\(y'=-3x^2-\left(m+1\right)\cdot2x+3\left(m+1\right)\)
=>\(y'=-3x^2+x\cdot\left(-2m-2\right)+\left(3m+3\right)\)
Để hàm số nghịch biến trên R thì \(y'< =0\forall x\)
=>\(\left\{{}\begin{matrix}\text{Δ}< =0\\a< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(-2m-2\right)^2-4\cdot\left(-3\right)\left(3m+3\right)< =0\\-3< 0\end{matrix}\right.\)
=>\(4m^2+8m+4+12\left(3m+3\right)< =0\)
=>\(4m^2+8m+4+36m+36< =0\)
=>\(4m^2+44m+40< =0\)
=>\(m^2+11m+10< =0\)
=>\(\left(m+1\right)\left(m+10\right)< =0\)
TH1: \(\left\{{}\begin{matrix}m+1>=0\\m+10< =0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>=-1\\m< =-10\end{matrix}\right.\)
=>\(m\in\varnothing\)
TH2: \(\left\{{}\begin{matrix}m+1< =0\\m+10>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< =-1\\m>=-10\end{matrix}\right.\)
=>-10<=m<=-1
b: \(y=-\dfrac{1}{3}x^3+mx^2-\left(2m+3\right)x\)
=>\(y'=-\dfrac{1}{3}\cdot3x^2+m\cdot2x-\left(2m+3\right)\)
=>\(y'=-x^2+2m\cdot x-\left(2m+3\right)\)
Để hàm số nghịch biến trên R thì \(y'< =0\forall x\)
=>\(\left\{{}\begin{matrix}\text{Δ}< =0\\a< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-1< 0\\\left(2m\right)^2-4\cdot\left(-1\right)\cdot\left(-2m-3\right)< =0\end{matrix}\right.\)
=>\(4m^2+4\left(-2m-3\right)< =0\)
=>\(m^2-2m-3< =0\)
=>(m-3)(m+1)<=0
TH1: \(\left\{{}\begin{matrix}m-3>=0\\m+1< =0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>=3\\m< =-1\end{matrix}\right.\)
=>\(m\in\varnothing\)
TH2: \(\left\{{}\begin{matrix}m-3< =0\\m+1>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< =3\\m>=-1\end{matrix}\right.\)
=>-1<=m<=3
L
1
13 tháng 11 2023
ĐKXĐ: m<>3
Để hàm số nghịch biến trên R thì \(\dfrac{1}{m-3}< 0\)
=>m-3<0
=>m<3
Chọn B