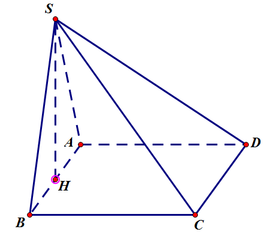
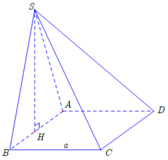
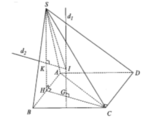
Cho hình chóp S.ABCD có đáy là hình vuông, mặt bên (SAB) là một tam giác đều nằm trong mặt phẳng vuông góc với mặt đáy (ABCD) và có diện tích bằng 27 3 4 (đvdt). Một mặt phẳng đi qua trọng tâm tam giác SAB và song song với mặt đáy (ABCD) chia khối chóp S.ABCD thành hai phần, tính thể tích V của phần chứa điểm S?
A. V = 24
B. V = 8
C. V = 12
D. V = 36


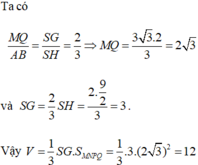

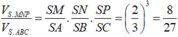
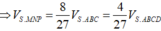
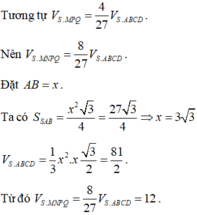

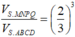
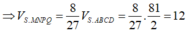


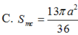
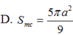

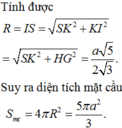


Đáp án là C
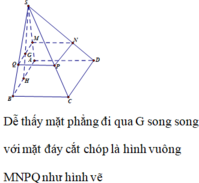
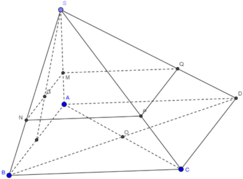
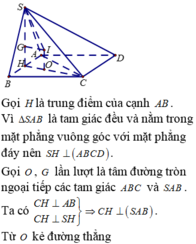
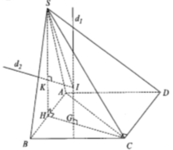
Cách 1. Ta có mặt phẳng (P) đi qua trọng tâm của tam giác SAB cắt các cạnh của khối chóp lần lượt tại M, N, P, Q. Với MN//AB, NP//BC, PQ//CD, QM//AD.
Tương tự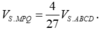
Nên
Đặt AB = x.
Ta có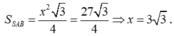
Từ đó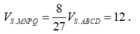
Cách 2. Do hai khối chóp S.MNPQ, S.ABCD đồng dạng với nhau theo tỉ số k = 2 3 nên tỉ lệ thể tích là