Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
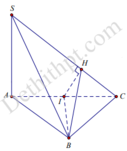
Vì Δ A B C cân tại B nên I là trung điểm của AC nên B I ⊥ A C .
Ta có:
S A ⊥ B I , B I ⊥ A C ⇒ B I ⊥ S A C ⇒ B I ⊥ S C
mà
S C ⊥ I H ⇒ S C ⊥ B I H ⇒ S B C ⊥ B I H .
Chọn D.
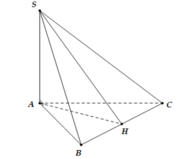
+) Ta có :
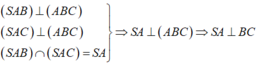
⇒ Suy ra : A đúng.
+) Ta có :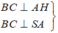 
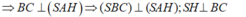
⇒ Suy ra : C đúng.
+) Mặt khác : AH ⊥ CD nên:
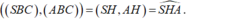
⇒ Suy ra : D sai.
Do SA ⊥ (ABCD) ⇒ \(\left\{{}\begin{matrix}SA\perp AB\\SA\perp AC\\SA\perp BC\end{matrix}\right.\)
Mà BC ⊥ AC ⇒ BC ⊥ (SAC) ⇒ BC ⊥ SC và BC ⊥ AH
Do BC ⊥ AH và AH ⊥ SC ⇒ AH ⊥ (SBC) ⇒ AH ⊥ KH ⇒ \(\widehat{AHK}=90^0\)
ΔSAB và ΔSAC vuông tại A
Mà AH và AK lần lượt là đường cao của ΔSAB và ΔSAC
⇒ \(\left\{{}\begin{matrix}SA^2=SK.SB\\SA^2=SH.SC\end{matrix}\right.\)
⇒ SK . SB = SH . SC
⇒ \(\dfrac{SK}{SH}=\dfrac{SC}{SB}\) ⇒ ΔSKH \(\sim\) ΔSCB ⇒ \(\widehat{SKH}=\widehat{SCB}=90^0\)
⇒ HK ⊥ SB
Mà AK⊥ SB
⇒ ((SAB),(SCB)) = (AK,AH) = \(\widehat{KAH}\) = 450 (đây là góc nhọn, vì \(\widehat{AHK}=90^0\))
⇒ ΔHAK vuông cân tại H ⇒ AK = \(\sqrt{2}AH\)
Ta có : \(\dfrac{S_{SAC}}{S_{SAB}}=\dfrac{\dfrac{1}{2}.AH.SC}{\dfrac{1}{2}AK.SB}=\dfrac{\dfrac{1}{2}.SA.AC}{\dfrac{1}{2}.SA.AB}\)
⇒ \(\dfrac{AH.SC}{AK.SB}=\dfrac{SA.AC}{SA.AB}\)
⇒ \(\dfrac{1}{\sqrt{2}}\) . \(\dfrac{SC}{SB}\) = \(\dfrac{AC}{AB}\). Mà AC = a và AB = 2a
⇒ \(\dfrac{1}{\sqrt{2}}\)\(\dfrac{SC}{SB}\) = \(\dfrac{1}{2}\) ⇒ \(\dfrac{SC^2}{SB^2}\) = \(\dfrac{1}{2}\) . Mà SB2 - SC2 = BC2 = 3a2
⇒ \(\left\{{}\begin{matrix}SC^2=3a^2\\SB^2=6a^2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}SB=a\sqrt{6}\\SC=a\sqrt{3}\end{matrix}\right.\) ⇒ SA = a\(\sqrt{2}\)
Từ đó ta tính được SH = \(\dfrac{2a\sqrt{3}}{3}\) và SK = \(\dfrac{a\sqrt{6}}{3}\)
Gọi M là trung điểm của SB thì ta có CM // HK (cùng vuông góc với SB)
Khoảng cách từ HK đến AC bằng khoảng cách từ HK đến (AMC)
