Tìm các giá trị của x trong khai triển ( 2 l g ( 10 - 3 x ) + 2 ( x - 2 ) l g 3 5 ) n biết rằng số hạng thứ 6 trong khai triển bằng 21 và C n 1 , C n 2 , C n 3 theo thứ tự lập thành một cấp số cộng
A. x= 4, x= 7
B. x= 3, x= 5
C. x= 0, x= 2
D. x= 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

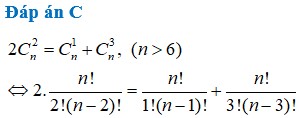
![]()
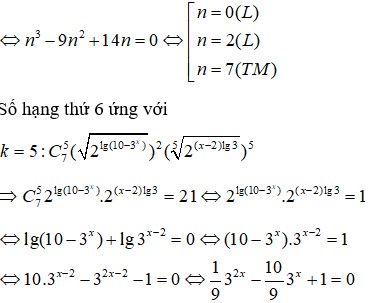
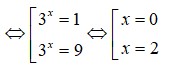

15/ Mũ 4=> có 4+1=5 số hạng=> số hạng chính giữa là: \(C^2_4.3^{4-2}.x^2.2^2y^2=58x^2y^2\)
18/ \(x.x^k=x^7\Rightarrow k=6\)
\(C^6_9.3^6.2^3=489888\)
19/ \(C^7_7+C^7_8.\left(-1\right)^7+C^7_9.2^2=...\)
C18 , c19 là lm sao vậy ạ ? Mk ko hiểu 2 bài này nơi

\(\left(x^2-x^3+1\right)^{10}=\sum\limits^{10}_{k=0}C_{10}^k\left(x^2-x^3\right)^k=\sum\limits^{10}_{k=0}C_{10}^k\sum\limits^k_{i=0}C_k^i.\left(x^2\right)^i.\left(-x^3\right)^{k-i}\)
\(=\sum\limits^{10}_{k=0}\sum\limits^k_{i=0}C_{10}^k.C_k^i.\left(-1\right)^{k-i}.x^{3k-i}\)
Số hạng chứa \(x^{10}\) thỏa mãn:
\(\left\{{}\begin{matrix}0\le k\le0\\0\le i\le k\\3k-i=10\end{matrix}\right.\) \(\Rightarrow\left(i;k\right)=\left(2;4\right);\left(5;5\right)\)
\(\Rightarrow\) Hệ số: \(C_{10}^4.C_4^2+C_{10}^5.C_5^5=...\)

\(\left(2x^3-\dfrac{3}{x^2}\right)^{10}=\sum\limits^{10}_{k=0}C^k_{10}.2^k.3^{10-k}.x^{3k}.\dfrac{1}{x^{2\left(10-k\right)}}\)
\(x^{10}=\dfrac{x^{3k}}{x^{20-2k}}\Leftrightarrow3k-20+2k=10\Leftrightarrow5k=30\Leftrightarrow k=6\)
\(\Rightarrow he-so:2^k.3^{10-k}=2^6.3^4=..\)

\(\left(x^2-2\right)^5=\sum\limits^5_{k=0}C_5^k\left(-2\right)^k\left(x^2\right)^{5-k}\)
\(=C_5^0x^{10}-C_5^1.2.x^8+C_5^2.2^2x^6-C_5^32^3x^4+C_5^42^4x^2-C_5^52^5\)

G(-2) = (-2)2 – 4 = 4 – 4 = 0;
G(1) = 12 – 4 = 1 – 4 = -3;
G(0) = 02 – 4 = 0 – 4 = -4;
G(1) = 12 – 4 = 1- 4 = -3;
G(2) = 22 – 4 = 4 – 4 = 0

\(4)D=x^2+x+1\)
\(D=x^2+2x.\frac{1}{2}+\left(\frac{1}{2}\right)^2-\left(\frac{1}{2}\right)^2+1\)
\(D=\left(x+\frac{1}{2}\right)^2-\frac{1}{4}+1\)
\(D=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\)
Vậy biểu thức trên luôn nhận giá trị dương với mọi giá trị của x.
Các câu khác lm tương tự nhé.
Cho góp ý xíu: lần sau bn đưa từng câu một lên diễn đàn thì sẽ có câu trả lời nhanh hơn là đưa cùng một lúc như thế này đấy
hok tốt~
\(D=x^2+x+1=x^2+x+\frac{1}{4}+\frac{3}{4}=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\)
\(\left(x+\frac{1}{2}\right)^2\ge0\forall x\Rightarrow\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\forall x\)( đpcm )
\(F=2x^2+4x+3=2\left(x^2+2x+1\right)+1=2\left(x+1\right)^2+1\)
\(2\left(x+1\right)^2\ge0\forall x\Rightarrow2\left(x+1\right)^2+1\ge1>0\forall x\)( đpcm )
\(G=3x^2-5x+3=3\left(x^2-\frac{5}{3}x+\frac{25}{36}\right)+\frac{11}{12}=3\left(x-\frac{5}{6}\right)^2+\frac{11}{12}\)
\(3\left(x-\frac{5}{6}\right)^2\ge0\forall x\Rightarrow3\left(x-\frac{5}{6}\right)^2+\frac{11}{12}\ge\frac{11}{12}>0\forall x\)( đpcm )
\(H=4x^2+4x+2=4\left(x^2+x+\frac{1}{4}\right)+1=4\left(x+\frac{1}{2}\right)^2+1\)
\(4\left(x+\frac{1}{2}\right)^2\ge0\forall x\Rightarrow4\left(x+\frac{1}{2}\right)^2+1\ge1>0\forall x\)( đpcm )
\(K=4x^2+3x+2=4\left(x^2+\frac{3}{4}x+\frac{9}{64}\right)+\frac{23}{16}=4\left(x+\frac{3}{8}\right)^2+\frac{23}{16}\)
\(4\left(x+\frac{3}{8}\right)^2\ge0\forall x\Rightarrow4\left(x+\frac{3}{8}\right)^2+\frac{23}{16}\ge\frac{23}{16}>0\forall x\)( đpcm )
\(L=2x^2+3x+4=2\left(x^2+\frac{3}{2}x+\frac{9}{16}\right)+\frac{23}{8}=2\left(x+\frac{3}{4}\right)^2+\frac{23}{8}\)
\(2\left(x+\frac{3}{4}\right)^2\ge0\forall x\Rightarrow2\left(x+\frac{3}{4}\right)^2+\frac{23}{8}\ge\frac{23}{8}>0\forall x\)( đpcm )