Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
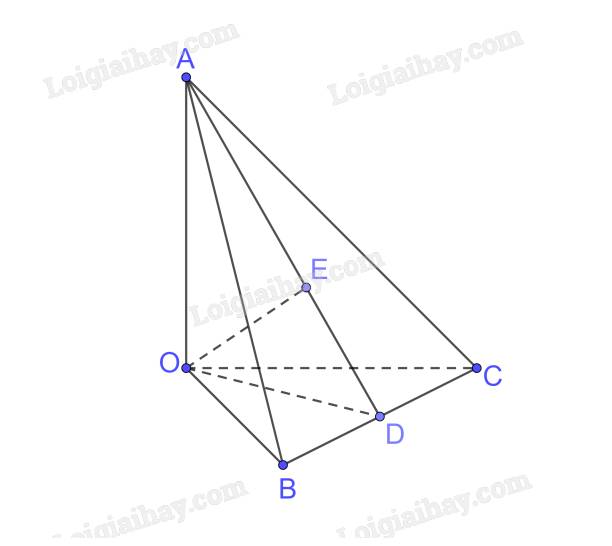
Ta có \(OA \bot OB,OA \bot OC \Rightarrow OA \bot \left( {OBC} \right);BC \subset \left( {OBC} \right) \Rightarrow OA \bot BC\)
Trong (OBC) kẻ \(OD \bot BC\)
\(\begin{array}{l} \Rightarrow BC \bot \left( {OAD} \right);BC \subset \left( {ABC} \right) \Rightarrow \left( {OAD} \right) \bot \left( {ABC} \right)\\\left( {OAD} \right) \cap \left( {ABC} \right) = AD\end{array}\)
Trong (OAD) kẻ \(OE \bot AD\)
\( \Rightarrow OE \bot \left( {ABC} \right) \Rightarrow d\left( {O,\left( {ABC} \right)} \right) = OE\)
Xét tam giác OBC vuông tại O có
\(\frac{1}{{O{D^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}} = \frac{1}{{{{\left( {a\sqrt 2 } \right)}^2}}} + \frac{1}{{{{\left( {2a} \right)}^2}}} = \frac{3}{{4{a^2}}} \Rightarrow OD = \frac{{2a\sqrt 3 }}{3}\)
Xét tam giác OAD vuông tại O có
\(\frac{1}{{O{E^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{D^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{{\left( {\frac{{2a\sqrt 3 }}{3}} \right)}^2}}} = \frac{7}{{4{a^2}}} \Rightarrow OE = \frac{{2a\sqrt 7 }}{7}\)
Vậy \(d\left( {O,\left( {ABC} \right)} \right) = \frac{{2a\sqrt 7 }}{7}\)
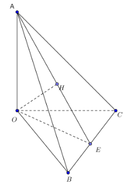
Qua B kẻ đường thẳng song song OM cắt OC kéo dài tại D
\(\Rightarrow OM||\left(ABD\right)\Rightarrow d\left(OM;AB\right)=d\left(OM;\left(ABD\right)\right)=d\left(O;\left(ABD\right)\right)\)
Gọi E là trung điểm BD, từ O kẻ \(OH\perp AE\)
\(BD||OM\) và M là trung điểm BC\(\Rightarrow OM\) là đường trung bình tam giác BCD
\(\Rightarrow BD=2OM=BC\Rightarrow\Delta BCD\) vuông cân tại B
O là trung điểm CD (do OM là đường trung bình BCD), E là trung điểm BD
\(\Rightarrow OE\) là đường trung bình tam giác BCD \(\Rightarrow\left\{{}\begin{matrix}OE=\dfrac{1}{2}BC=\dfrac{a\sqrt{2}}{2}\\OE||BC\Rightarrow OE\perp BD\end{matrix}\right.\)
\(\left\{{}\begin{matrix}OA\perp OB\\OA\perp OC\end{matrix}\right.\) \(\Rightarrow OA\perp\left(OBC\right)\Rightarrow OA\perp BD\)
\(\Rightarrow BD\perp\left(OAE\right)\Rightarrow BD\perp OH\)
\(\Rightarrow OH\perp\left(ABD\right)\Rightarrow OH=d\left(O;\left(ABD\right)\right)\)
Áp dụng hệ thức lượng trong tam giác vuông OAE:
\(OH=\dfrac{OA.OE}{AE}=\dfrac{OA.OE}{\sqrt{OA^2+OE^2}}=\dfrac{a\sqrt{3}}{3}\)
Đáp án D
Gọi H là hình chiếu của O xuống (ABC)
Ta có: 1 O H 2 = 1 a 2 + 1 2 a 2 + 1 a 3 2 = 19 12 a 2 ⇒ O H = 2 a 3 19
Đáp án A
Gọi H là hình chiếu của O lên mặt phẳng (ABC) nên O H ⊥ A B C ⇒ O H ⊥ B C 1 .
Mặt khác O A ⊥ O B , O A ⊥ O C ⇒ O A ⊥ O B C ⇒ O A ⊥ B C 2 .
Từ (1),(2) suy ra B C ⊥ A O H ⇒ B C ⊥ A H . Chứng minh tương tự ta được A B ⊥ C H . Suy ra H là trực tâm của ΔABC.
Trong mặt phẳng (ABC) gọi E là giao điểm của AH và BC.
Ta có O H ⊥ A B C ⇒ O H ⊥ A E tại H.
O A ⊥ A B C ⇒ O A ⊥ O E tức là OH là đường cao của tam giác vuông OAE.
Mặt khác OE là đường cao của tam giác vuông OBC.
Do đó: 1 O H 2 = 1 O A 2 + 1 O E 2 = 1 O A 2 + 1 O B 2 + 1 O C 2 .
⇔ 1 d 2 = 1 a 2 + 1 b 2 + 1 c 2 ⇒ d = a b c b 2 c 2 + a 2 c 2 + a 2 b 2 .
Đáp án D
Ta có: V O . A B C = 1 6 O A . O B . O C = 6 ⇒ O C = 3
Lại có 1 d O ; A B C 2 = 1 O A 2 + 1 O B 2 + 1 O C 2 ⇒ d O ; A B C = 12 41
Chọn B