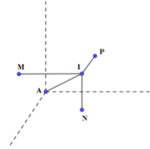
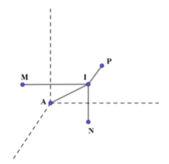
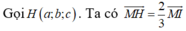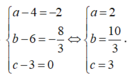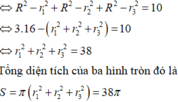Trong không gian Oxyz, cho mặt cầu (S): (x-1)2+ (y-2)2+ z2=25 và một điểm A(a,b,c) nằm trên mặt cầu (S). Từ A vẽ ba tia đôi một vuông góc với nhau cắt mặt cầu (S) tại điểm thứ hai là M, N, P. Biết rằng mặt phẳng (MNP) luôn đi qua một điểm cố định K(1;1;3). Giá trị của biểu thức a + 7b + c bằng
A. 3
B. 4
C. 6
D. 9