Trong các hàm số sau, hàm số nào có tập xác định là R?
A. y = x 1 3
B. y = ln x
C. y = log x 2
D. y = 3 x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

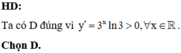

Chọn D. Bởi vì hàm số ln x luôn luôn dương nên chắc chắn sẽ đồng biến trên TXĐ của nó

a, Điều kiện: \(2^x\ne3\Rightarrow x\ne log_23\)
Vậy D = R \ \(log_23\)
b, Điều kiện: \(25-5^x\ge0\Rightarrow5^x\le5^2\Rightarrow x\le2\)
Vậy D = \((-\infty;2]\)
c, Điều kiện: \(\left\{{}\begin{matrix}x>0\\lnx\ne1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x>0\\x\ne e\end{matrix}\right.\)
Vậy D = \(\left(0;+\infty\right)\backslash\left\{e\right\}\)
d, Điều kiện: \(\left\{{}\begin{matrix}x>0\\1-log_3x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x>0\\log_3x\le1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x>0\\x\le3\end{matrix}\right.\Rightarrow0< x\le3\)
Vậy D = \((0;3]\)

a, \(y=log\left|x+3\right|\) có nghĩa khi \(\left|x+3\right|>0\)
Mà \(\left|x+3\right|\ge0\forall x\in R\)
\(\Rightarrow\) \(\left|x+3\right|>0\) khi \(x\ne-3\)
Vậy tập xác định của hàm số là D = R \ {-3}.
b, \(y=ln\left(4-x^2\right)\) có nghĩa khi \(4-x^2>0\)
\(\Rightarrow x^2< 4\\ \Leftrightarrow-2< x< 2\)
Vậy tập xác định của hàm số là D = (-2;2).

Hàm số a,b là các hàm số logarit
a: \(log_{\sqrt{3}}x\)
Cơ số là \(\sqrt{3}\)
b: \(log_{2^{-2}}x\)
Cơ số là \(2^{-2}=\dfrac{1}{4}\)

\(\dfrac{\sqrt{3}}{2}< 1;\dfrac{\sqrt[3]{26}}{3}< 1;\pi>1;\dfrac{\sqrt{15}}{4}< 1\)
Hàm số đồng biến là: \(log_{\pi}x\)
Hàm số nghịch biến là: \(\left(\dfrac{\sqrt{3}}{2}\right)^x;\left(\dfrac{\sqrt[3]{26}}{3}\right)^x;log_{\dfrac{\sqrt{15}}{4}}x\)

Ta có: \(y = \cos x\)
\(y\left( { - x} \right) = \cos \left( { - x} \right) = \cos x = y\)
Suy ra hàm số \(y = \cos x\) là hàm số chẵn
Vậy ta chọn đáp án C

a: TXĐ: \(D=R\backslash\left\{-\dfrac{1}{2}\right\}\)
b: TXĐ: \(D=R\backslash\left\{-3;1\right\}\)
c: TXĐ: \(D=\left[-\dfrac{1}{2};3\right]\)

a: Đây là hàm số bậc nhất
a=2; b=-3
b: Đây là hàm số bậc nhất
a=-6; b=-7
c: Đây ko là hàm số bậc nhất

\(a,D=R\\ b,2x-3>0\\ \Rightarrow x>\dfrac{3}{2}\\ \Rightarrow D=(\dfrac{3}{2};+\infty)\\ c,-x^2+4>0\\ \Rightarrow x^2< 4\\ \Leftrightarrow-2< x< 2\\ \Rightarrow D=\left(-2;2\right)\)