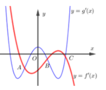
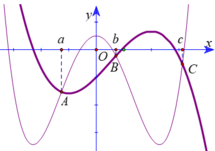
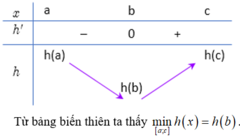
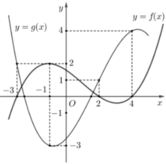
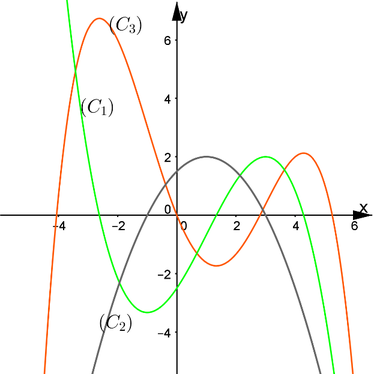
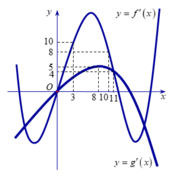
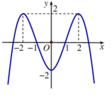
Cho hàm số y = f x v à y = g x là hai hàm liên tục trên R có đồ thị hàm số y = f ' x là đường cong nét đậm và y = g ' x là đường cong nét mảnh như hình vẽ. Gọi 3 giao điểm A, B, C của đồ thị y = f ' x v à y = g ' x trên hình vẽ lần lượt có hoành độ là a, b, c. Tìm giá trị nhỏ nhất của hàm số h x = f x − g x trên đoạn a ; c ?
A. M i n a ; c h x = h 0
B. M i n a ; c h x = h a
C. M i n a ; c h x = h b
D. M i n a ; c h x = h c
.
.
.
.
.
tương ứng là 
.
có các điểm cực trị có hoành độ là nghiệm của phương trình 
nên hàm số 
là đạo hàm của hàm số 
.
có các điểm cực trị có hoành độ là nghiệm của phương trình 
nên hàm số 
là đạo hàm của hàm số 
.
, 
và 
theo thứ tự, lần lượt tương ứng với đường cong 
.
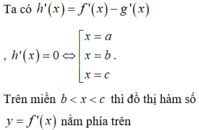
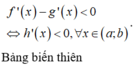
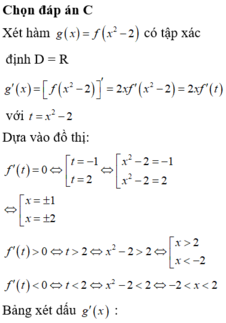
Đáp án C
Ta có: h ' x = f ' x − g ' x = 0 ⇔ x = a x = b x = c
Với x ∈ a ; b thì đồ thị g ' x nằm trên f ' x nên g ' x > f ' x ⇒ h ' x < 0 hàm số nghịch biến trên đoạn a ; b
Tương tự với x ∈ b ; c thì h x đồng biến.
Do đó M i n a ; c h x = h b .