Viết phương trình mặt phẳng (P) đi qua ba điểm A 1 ; 0 ; 0 , B 0 ; - 2 ; 0 và C(0;0;4)
![]()
![]()
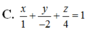
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

để ý rằng 6x+3y+2z-6=0 \(\Leftrightarrow\frac{x}{1}+\frac{y}{2}+\frac{z}{3}=1\)nên ta có ngay kết quả cơ bản sau: mặt phẳng (P) đi qua ba điểm A(a;0;0), B(0;b;0) và C(0;0;c) với abc\(\ne\)0 có phương trình
\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\)

Cách 1:
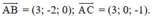
Mặt phẳng (R) đi qua ba điểm A, B, C nhận 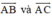 là hai vec tơ chỉ phương
là hai vec tơ chỉ phương
⇒ Nhận 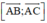 = ((-2).(-1) – 0; 0.3 – 3.(-1); 3.0 – 3.(-2)) = (2; 3; 6) là vec tơ pháp tuyến.
= ((-2).(-1) – 0; 0.3 – 3.(-1); 3.0 – 3.(-2)) = (2; 3; 6) là vec tơ pháp tuyến.
(R) đi qua A(-3; 0; 0) nên có phương trình:
2(x + 3) + 3y + 6z = 0
⇔ 2x + 3y + 6z + 6 = 0.
Cách 2 :
(R) đi qua A(-3 ; 0 ; 0) ; B(0 ; -2 ; 0) ; C(0 ; 0 ; -1) nên có phương trình đoạn chắn là :
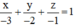
⇔ 2x + 3y + 6z + 6 = 0.

Chọn C
Gọi tâm mặt cầu I(x;-x+2z-4;z). Tìm x,z từ hệ hai phương trình IA=IB=IC

Chọn D.
Ta có: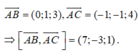
Gọi n → là một vectơ pháp tuyến của mặt phẳng (ABC) ta có

![]() ta được phương trình mặt phẳng (ABC) là:
ta được phương trình mặt phẳng (ABC) là:
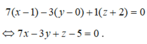

a.
Gọi phương trình đường tròn (C) có dạng:
\(x^2+y^2-ax-by+c=0\)
Do A;B;C thuộc (C) nên: \(\left\{{}\begin{matrix}0+16-0.a-4b+c=0\\9+16-3a-4b+c=0\\9+0-3a-0.b+c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-4b+c=-16\\-3a-4b+c=-25\\-3a+c=-9\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=3\\b=4\\c=0\end{matrix}\right.\)
Hay pt (C) có dạng: \(x^2+y^2-3x-4y=0\)
b.
Đường tròn (C) tiếp xúc (d) nên có bán kính \(R=d\left(C;d\right)=\dfrac{\left|3.3+0.4-5\right|}{\sqrt{3^2+4^2}}=\dfrac{4}{5}\)
Phương trình: \(\left(x-3\right)^2+y^2=\dfrac{16}{25}\)
Chọn đáp án C