Cho hàm số y = x 4 - 2 ( m + 2 ) x 2 + 3 ( m + 2 ) 2 . Đồ thị của hàm số trên có ba cực trị tạo thành tam giác đều. Tìm mệnh đề đúng
A. m ∈ (0;1)
B. m ∈ (-2;-1)
C. m ∈ (1;2)
D. m ∈ (-1;0)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét hàm số \(y=ax^4+bx^2+c\)
Ta có \(y'=4ax^3+2bx=2x\left(2ax^2+b\right)\)
\(y'=0\Leftrightarrow x=0\) hoặc \(2ax^2+b=0\left(1\right)\)
Đồ thị hàm số có 3 cực trị phân biệt khi và chỉ khi \(y'=0\) có 3 nghiệm phân biệt hay phương trình (1) có 2 nghiệm phân biệt khác 0 \(\Leftrightarrow ab< 0\) (*)
Với điều kiện (*) thì đồ thị có 3 điểm cực trị là :
\(A\left(0;c\right);B\left(-\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right);C\left(\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right)\)
Ta có \(AB=AC=\sqrt{\frac{b^2-8ab}{16a^2}};BC=\sqrt{-\frac{2b}{a}}\) nên tam giác ABC vuông khi và chỉ khi vuông tại A.
Khi đó \(BC^2=2AB^2\Leftrightarrow b^3+8a=0\)
Do đó yêu cầu bài toán\(\Leftrightarrow\begin{cases}ab< 0\\b^3+8a=0\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\-8\left(m+1\right)^3+8=0\end{cases}\)\(\Leftrightarrow m=0\)
b) Ta có yêu cầu bài toán \(\Leftrightarrow\begin{cases}ab< 0\\OA=BC\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\m^2-4\left(m+1\right)=0\end{cases}\)
\(\Leftrightarrow m=2\pm2\sqrt{2}\)

Đáp số : \(m=-\frac{1}{\sqrt[3]{3}};m=-\sqrt[3]{\left(2+\sqrt{3}\right)^2}\)

Hàm số có cực đại, cực tiểu khi m<2. Tọa độ các điểm cực trị là :
\(A\left(0;m^2-5m+5\right);B\left(\sqrt{2-m};1-m\right);C\left(-\sqrt{2-m};1-m\right)\)

Đáp án D
C m có 3 điểm cực trị tạo thành tam giác vuông thì b 3 a = − 8
⇔ 2 m 3 − 1 = − 8 ⇔ 8 m 3 = 8 ⇔ m = 1
Đáp án là D
Đồ thị hàm bậc 4 trùng phương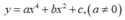 có ba điểm cực trị tạo thành một tam giác đều
có ba điểm cực trị tạo thành một tam giác đều