gải và biện luận pt theo tham số m
b) (m+1)x-2m+1=3x
NHANH NHÉ,MÌNH ĐANG RẤC GẤP Ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NH
2
Những câu hỏi liên quan
4 tháng 3 2022
x= 3m-3/m-2
Tại m =2 thì pt vô nghiệm
Tại m khác 2 thì có nghiệm duy nhất vì đây là hàm bậc nhất
PT
1
CM
22 tháng 8 2019
(2m + 1)x – 2m = 3x – 2
⇔ (2m + 1)x – 3x = 2m – 2
⇔ (2m + 1 – 3).x = 2m – 2
⇔ (2m – 2).x = 2m – 2 (3)
+ Xét 2m – 2 ≠ 0 ⇔ m ≠ 1, pt (3) có nghiệm duy nhất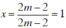 
+ Xét 2m – 2 = 0 ⇔ m = 1, pt (3) ⇔ 0.x = 0, phương trình có vô số nghiệm.
Kết luận :
+ Với m = 1, phương trình có vô số nghiệm
+ Với m ≠ 1, phương trình có nghiệm duy nhất x = 1.
VD
21 tháng 3 2022
a, \(\Delta'=\left(m-1\right)^2-\left(-2m+5\right)=m^2-2m+1+2m-5=m^2-4\)
Để pt vô nghiệm thì \(m^2-4< 0\Leftrightarrow-2< m< 2\)
Để pt có nghiệm kép thì \(m^2-4=0\Leftrightarrow m=\pm2\)
Để pt có 2 nghiệm phân biệt thì \(m^2-4>0\Leftrightarrow\left[{}\begin{matrix}m< -2\\m>2\end{matrix}\right.\)
2, Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m-2\\x_1x_2=-2m+5\end{matrix}\right.\)
\(a,ĐKXĐ:x_1,x_2\ne0\\ \dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}=2\\ \Leftrightarrow\dfrac{x_1^2+x_2^2}{x_1x_2}=2\\ \Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=0\\ \Leftrightarrow\left(2m-2\right)^2-4\left(-2m+5\right)=0\\ \Leftrightarrow4m^2-8m+4+8m-20=0\\ \Leftrightarrow4m^2-16=0\\ \Leftrightarrow m=\pm2\)
\(b,x_1+x_2+2x_1x_2\le6\\ \Leftrightarrow2m-2+2\left(-2m+5\right)\le6\\ \Leftrightarrow2m-2-4m+10-6\le0\\ \Leftrightarrow-2m+2\le0\\ \Leftrightarrow m\ge1\)
BD
18 tháng 3 2018
(a=m,b=-2m+1,c=m+2)
∆=b^2 - 4ac
=(-2m+1)^2 - 4×m×(m+2)
=4m^2-2m-2m+1-4m^2-8m
=-12m+1
<+> Để pt có 2 nghiệm phân biệt thì:∆>0 <=> -12m+1>0 <=> m<1/12
Vậy m<1/12 thì pt có 2 nghiệm phân biệt
<+> Để pt có nghiệm kép thì :∆=0 <=>-12m+1=0 <=>m=1/12
Vậy m=1/12 thì pt có nghiệm kép
<+> Để pt vô nghiệm thì :∆<0 <=> -12m+1<0 <=> m>1/12
Vậy m>1/12 thì pt vô nghiệm
CM
23 tháng 1 2017
m = 0 phương trình trở thành
-x - 2 = 0 ⇒ x = -2
m ≠ 0 phương trình đã cho là phương trình bậc hai, có Δ = 4m + 1
Với m < -1/4 phương trình vô nghiệm;
Với m ≥ -1/4 nghiệm của phương trình là
HH
0
7 tháng 3 2021
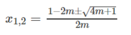
Với m = 1 hoặc m = -1 ta có:
0x = m
\(\Rightarrow\) m = 0
Với m \(\ne\) \(\pm1\) ta có:
x = \(\dfrac{m}{m^2-1}=\dfrac{m}{\left(m+1\right)\left(m-1\right)}\)
Vậy ...
Chúc bn học tốt! (Chắc vậy!)
TD
0
\(PT\Leftrightarrow\left(m+1\right)x-3x=2m-1\\ \Leftrightarrow x\left(m-2\right)=2m-1\\ \Leftrightarrow x=\dfrac{2m-1}{m-2}\left(m\ne2\right)\)