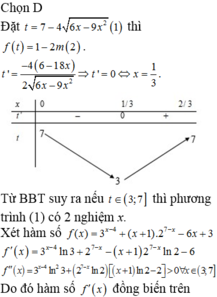
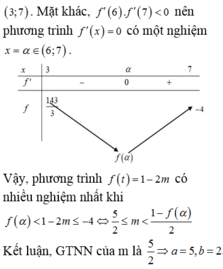
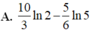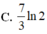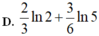Cho hàm số f ( x ) = 3 x - 4 + ( x + 1 ) . 2 7 - x - 6 x + 3 . Giả sử m 0 = a b a , b ∈ ℤ , a b l à p h â n s ố t ố i g i ả n là giá trị nhỏ nhất của tham số thực m sao cho phương trình f 7 - 4 6 x - 9 x 2 + 2 m - 1 = 0 có số nghiệm nhiều nhất. Tính giá trị của biểu thức P = a + b 2
A. 11
B. 7
C. -1
D. 9