Cho hàm số y = f x thỏa mãn f ' x = - x 2 - 2 ∀ x ∈ ℝ . Bất phương trình f(x)<m có nghiệm thuộc khoảng (0;1) khi và chỉ khi
A. m ≥ f 1
B. m ≥ f 0
C. m>f(0)
D. m>f(1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
11 tháng 1 2017
Đúng(0)
Những câu hỏi liên quan
CM
15 tháng 6 2019
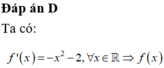
Đáp án D
Ta có f ' x = - e x . f 2 x ⇔ - f ' x f 2 x = e x ⇔ ∫ - f ' x f 2 x d x = ∫ e x d x ⇔ 1 f x = e x + C
Mà f 0 = 1 2 ⇒ 1 f 0 = e 0 + C ⇔ C + 1 = 2 ⇒ C = 1 → f x = 1 e x + 1
Do đó f ' x = - e x e x + 1 2 ⇒ f ' ln 2 = - 2 9 . Vậy phương trình tiếp tuyến là 2 x + 9 y - 2 ln 2 - 3 = 0 .
CM
30 tháng 8 2019
Đáp án A
Đặt f 1 = a f ' 1 = b , thay x = 0 vào giả thiết, ta được f 2 1 = - f 3 0 ⇔ a 3 + a 2 = 0 ⇔ [ a = 0 a = - 1
Đạo hàm cả 2 vế biểu thức f 2 1 + 2 x = x - f 3 1 - x , ta đưuọc
4 f ' 1 + 2 x . f 1 + 2 x = 1 + 3 f ' 1 - x . f 2 1 - x 1
Thay x = 0 vào (1), ta có 4 f ' 1 . f 1 = 1 + 3 f ' 1 . f 2 1 ⇔ 4 a b = 1 + 3 a 2 b 2
TH1. Với a = 0 thay vào (2), ta được 0 = 1 (vô lí)
TH2. Với a = -1 thay vào (2), ta được - 4 b = 1 + 3 b ⇔ b = - 1 7 ⇒ f ' 1 = - 1 7
Vậy phương trình tiếp tuyến cần tìm là y - f 1 = f ' 1 x - 1 ⇒ y = - 1 7 x - 6 7 .
CM
17 tháng 1 2019
Đáp án C
Với f x > 0 , ∀ x ∈ ℝ . Xét biểu thức f ' x f x = 2 - 2 x *
Lấy nguyên hàm 2 vế (*), ta được ∫ d f x f x = ∫ 2 - 2 x d x
⇔ ∫ d f x f x = - x 2 + 2 x + C ⇔ ln f x = - x 2 + 2 x + C
Mà f(0) =1 suy ra C = lnf(0) = ln1 = 0. Do đó f x = e - x 2 + 2 x
Xét hàm số f x = e - x 2 + 2 x trên - ∞ ; + ∞ , có f ' x = - 2 x + 2 = 0 ⇔ x = 1
Tính giá trị f 1 = e ; lim x → - ∞ f x = 0 ; lim x → - ∞ f x = 0
Suy ra để phương trình f(x) = m có hai nghiệm thực phân biệt ⇔ 0 < m < e .
CM
1 tháng 6 2017
Đáp án B
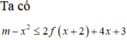
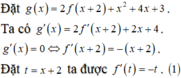
(1) là phương trình hoành độ giao điểm của đồ thị f'(t) và đường thẳng d : y = -t (hình vẽ)
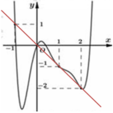
Dựa vào đồ thị của f'(t) và đường thẳng y =-t ta có
