Hình vẽ sau là đồ thị của ba hàm số y = x α , y = x β , y = x γ (với x>0 ) và α , β , γ là các số thực cho trước.
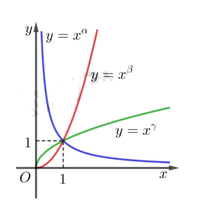
Mệnh đề nào dưới đây đúng?
C. α > β > γ
D. β > γ > α
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Với x > 1 mà lim x α = 0 ⇔ 0 < a < 1 và cũng suy ra β , γ > 1
Với x > 1 , với cùng 1 giá trị x 0 thì x β > x γ ⇒ β > γ .

a) - Với hàm số y = x + 1
Cho x = 0 y = 1 được A(0; 1)
Cho y = 0 x = -1 được B(-1; 0)
Nối A, B được đường thẳng y = x + 1
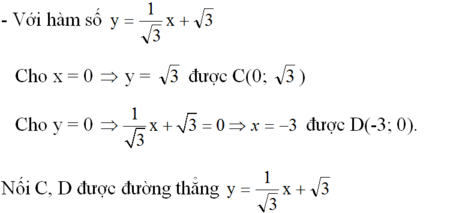
- Với hàm số y = √3 x - √3
Cho x = 0 => y = -√3 được E(0; -√3)
Cho y = 0 => x = 1 được F(1; 0).
Nối E, F được đường thẳng y = √3 x - √3
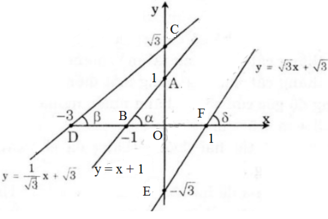
b) Ta có:
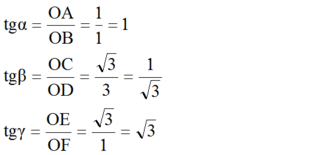
Suy ra α = 45o, β = 30o, γ = 60o

a) Đúng.
(α) ⊥ (β) ⇒ ∃ đường thẳng d ⊂ (β) và d ⊥ (α ).
Mà (α ) // (γ)
⇒ d ⊥ (γ)
⇒ (β) ⊥ (γ).
b) Sai, vì hai mặt phẳng (β), (γ) cùng vuông góc với mp(α) có thể song song hoặc cắt nhau.

Đáp án D.
Ta có log x a = 1 α ; log x b = 1 β ; log x c = 1 γ
⇒ log x a + log x b + log x c = 1 α + 1 β + 1 γ ⇒ log x a b c = α β + β γ + γ α α β γ
⇔ log a b c x = α β γ α β + β γ + γ α .
Đáp án D
Hàm số x α nghịch biến do đó 0 < α < 1 .
Các hàm số x β , x γ là các hàm số đồng biến do đó β , γ > 1 .
Cho x = 100 ⇒ 100 β > 100 γ ⇒ β > γ .