Cho hình lăng trụ tam giác đều ABC.A'B'C' có
A
B
=
2
3
,
A
A
'
=
2
. Gọi M, N, P lần lượt là trung điểm của các cạnh A'B',A'C' và BC (tham khảo hình vẽ bên). Côsin của góc tạo bởi hai mặt phẳng ( AB'C' ) và ( MNP ) bằng A.
6
13
65
B.
13
65
C.
17
13
65
D.
18
13
65
...
Đọc tiếp
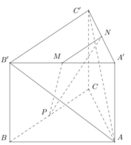
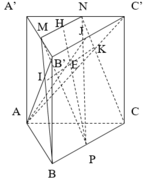
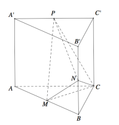
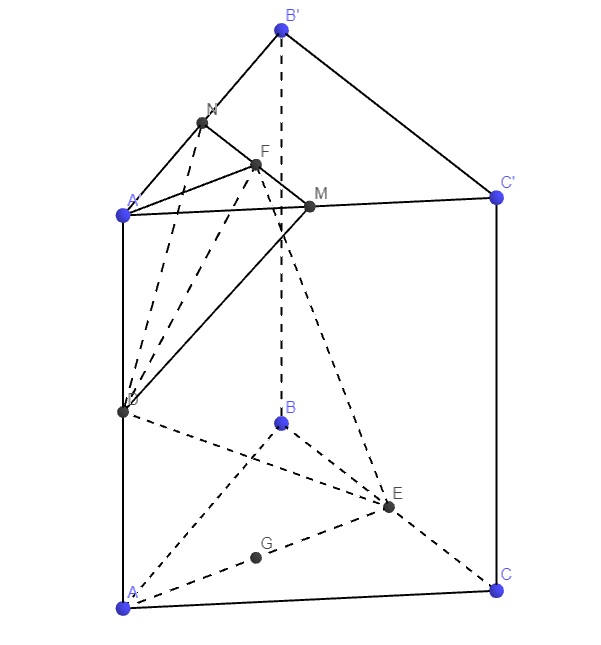
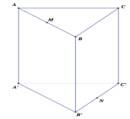
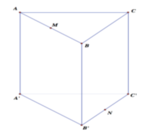
Cho hình lăng trụ tam giác đều ABC.A'B'C' có A B = 2 3 , A A ' = 2 . Gọi M, N, P lần lượt là trung điểm của các cạnh A'B',A'C' và BC (tham khảo hình vẽ bên). Côsin của góc tạo bởi hai mặt phẳng ( AB'C' ) và ( MNP ) bằng
A. 6 13 65
B. 13 65
C. 17 13 65
D. 18 13 65
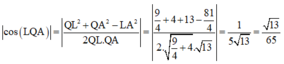
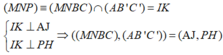
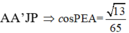
Dùng phương pháp tọa độ hóa.
Đặt hệ trục tọa độ, ở đây như thầy đã trình bày ta nên chọn gốc tại P trục Ox, Oy là PA và PC.
Gọi α góc tạo bởi hai mặt phẳng ( AB'C' ) và (MNP)
Khi đó cos α = n 1 → . n 2 → n 1 → . n 2 → = 13 65
Đáp án cần chọn là B