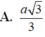
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Gọi I là trung điểm BC; kẻ G H ⊥ A C = H
Xét ∆ A B C vuông cân tại C ta có:
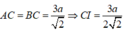
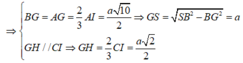
Kẻ G K ⊥ S H = K ⇒ G K ⊥ m p ( S A C )
Xét ∆ S G H vuông tại G có:
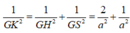
⇒ G K = a 3 3
⇒ d ( B , m p ( S A C ) ) = 3 G K = a 3 ( đ v đ d )
Vì tam giác ABC vuông cân tại C, \(AB=3a\Rightarrow CA=CB=\frac{3a}{\sqrt{2}}\)
Gọi M là trung điểm \(AC\Rightarrow MC=\frac{3a}{2\sqrt{2}}\Rightarrow MB=\frac{3a\sqrt{5}}{2\sqrt{2}}\)
\(\Rightarrow BG=\frac{2}{3}BM=\frac{a\sqrt{5}}{\sqrt{2}}\Rightarrow SG=\sqrt{SB^2-BG^2}=a\)
\(\Rightarrow V_{S.ABC}=\frac{1}{3}SG.S_{\Delta ABC}=\frac{3a^2}{4}=\frac{3a^2}{4}\)
Kẻ \(GI\perp AC\left(I\in AC\right)\Rightarrow AC\perp\left(SGI\right)\)
Ta có : \(GI=\frac{1}{3}BC=\frac{a}{\sqrt{2}}\)
Kẻ \(GH\perp SI\left(H\in SI\right)\Rightarrow GH\perp\left(SAC\right)\Rightarrow d\left(G,\left(SAC\right)\right)=GH\)
Ta có \(\frac{1}{GH^2}=\frac{1}{GS^2}+\frac{1}{GI^2}\Rightarrow GH=\frac{a}{\sqrt{3}}\Rightarrow3d\left(B,\left(SAC\right)\right)=3GH=a\sqrt{3}\)
Đáp án B
Gọi H là chân đường vuông góc hạ từ đỉnh S lên mặt phẳng (ABC), khi đó ta chứng minh được H là trung điểm của BC. Gọi M là trung điểm của AB khi đó từ giả thiết ta có: 
Đặt AB = x ta tính được: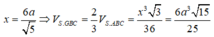 
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC=d\left(C;\left(SAB\right)\right)\)
Gọi D là trung điểm AB, theo tính chất trọng tâm: \(GD=\dfrac{1}{3}CD\)
\(\Rightarrow d\left(G;\left(SAB\right)\right)=\dfrac{1}{3}d\left(C;\left(SAB\right)\right)=\dfrac{1}{3}BC=\dfrac{1}{3}AB=\dfrac{a}{3}\)
Đáp án B