Cho hình chóp S.ABCD. có đáy ABCD là hình bình hành, E là trung điểm của SA, F, G lần lượt là các điểm thuộc cạnh BC, CD C F < F B ; G C < G D . Thiết diện của hình chóp cắt bởi E F G là
A. Tam giác
B. Tứ giác
C. Ngũ giác
D. Lục giác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C
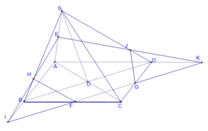
Trong mp (ABCD), gọi

Do đó ngũ giác EHFGJ là thiết diện của hình chóp cắt bởi (EFG)

Đáp án C
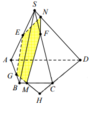
Kẻ EG cắt SB tại I, nối FI cắt BC tại M.
Kẻ GM cắt CD tại H, nối FH cắt SD tại N
Vậy thiết diện cần tìm là ngũ giác GMFNE (hình vẽ bên)

Qua F kẻ đường thẳng song song AD cắt AB tại H
\(\Rightarrow\left(FGH\right)||\left(SBC\right)\Rightarrow GH||\left(SBC\right)\Rightarrow GH||BC\)
Đặt \(\widehat{BAE}=a\) ; \(\widehat{DAF}=b\) (để đỡ dài)
Ta có: \(a+b=90^0-\widehat{EAF}=45^0\)
\(\Rightarrow tan\left(a+b\right)=tan45^0\)
\(\Rightarrow\dfrac{tana+tanb}{1-tana.tanb}=1\)
\(\Rightarrow tana+tanb=1-tana.tanb\)
\(\Rightarrow tanb=\dfrac{1-tana}{1+tana}\)
Mà \(tana=tan\widehat{BAE}=\dfrac{BE}{AB}=\dfrac{1}{2}\)
\(\Rightarrow tanb=tan\widehat{DAF}=\dfrac{DF}{AD}=\dfrac{AH}{AB}=\dfrac{1-\dfrac{1}{2}}{1+\dfrac{1}{2}}=\dfrac{1}{3}\)
\(\Rightarrow3AH=AB=AH+BH\Rightarrow2AH=BH\Rightarrow\dfrac{AH}{BH}=\dfrac{1}{2}\)
Talet: \(\dfrac{GA}{GS}=\dfrac{AH}{BH}=\dfrac{1}{2}\)

Đáp án A
Dễ thấy SAEC = 1 2 SABC = 1 4 SABCD
=> SAECF = 1 2 SABCD
VS.AECF = 1 2 VS.ABC

Đề bài sai òi :v Vẽ hình ra đi bạn.
Giờ tui gán MN vô (SBD) thì giao tuyến của (SBD) và (SBC) là SB. Vậy nên SB phải song song với MN. Nhưng ko :) Song song chết liền hà :)
Chọn C.
Phương pháp : Dựng thiết diện.
Cách giải : Gọi I, J lần lượt là giao điểm của GF với AB và AD.
Gọi H là giao điểm của IE và SB.
Gọi K là giao điểm của SD và EJ.
Suy ra thiết diện cần tìm là ngũ giác EHFGK.