Tại mặt nước, hai nguồn kết hợp được đặt ở A và B cách nhau 68 mm, dao động điều hòa cùng tần số, cùng pha, theo phương vuông góc với mặt nước. Trên đoạn AB, hai phần tử nước dao động với biên độ cực đại có vị trí cân bằng cách nhau một đoạn ngắn nhất là 10 mm. Điểm C là vị trí cân bằng của phần tử ở mặt nước sao cho AC ⊥ BC. Phần tử nước ở C dao động với biên độ...
Đọc tiếp
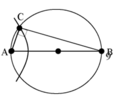
Tại mặt nước, hai nguồn kết hợp được đặt ở A và B cách nhau 68 mm, dao động điều hòa cùng tần số, cùng pha, theo phương vuông góc với mặt nước. Trên đoạn AB, hai phần tử nước dao động với biên độ cực đại có vị trí cân bằng cách nhau một đoạn ngắn nhất là 10 mm. Điểm C là vị trí cân bằng của phần tử ở mặt nước sao cho AC ⊥ BC. Phần tử nước ở C dao động với biên độ cực đại. Khoảng cách BC lớn nhất bằng
A. 37,6 mm.
B. 67,6 mm
C. 64,0 mm.
D. 68,5 mm
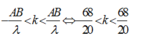
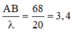
Đáp án B
2 điểm dao động cực đại trên AB cách nhau ngắn nhất 1 đoạn λ/2 =>λ = 20 mm.
Có A B λ = 3 ⇒ Trên mỗi phía của đường trung trực của đoạn AB có 3 đường cực đại.
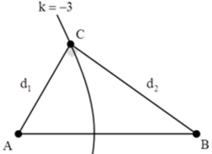
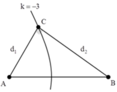
Có AC vuông góc với BC nên C thuộc đường tròn đường kính AB. BC lớn nhất thì C phải gần A nhất, tức là C thuộc dãy cực đại thứ 3.
Suy ra C B − C A = 3 λ = 60 . Mặt khác, với Pytago có C A 2 + C B 2 = 68 2 .
Dễ dàng giải hệ này ta tìm được BC = 67,58 (mm)