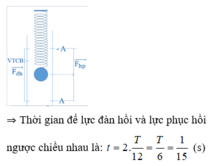
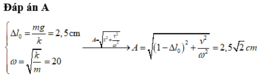Một con lắc lò xo treo thẳng đứng, lò xo có khối lượng không đáng kể, k = 50 N/m, m = 200 g. Vật đang nằm yên ở vị trí cân bằng thì được kéo thẳng đứng xuống dưới để lò xo dãn 12 cm rồi thả cho nó dao động điều hòa. Lấy g = π 2 m / s 2 . Thời gian lực đàn hồi tác dụng vào vật ngược chiều với lực phục hồi trong một chu kì là
A. 1/30 s
B. 2/15 s
C. 1/10 s
D. 1/15 s