Cho khối hộp ABCD.A’B’C’D’. Gọi M là trung điểm của AB. Mặt phẳng (MB’D’) chia khối hộp thành hai phần. Tính tỉ số thể tích hai phần đó
A. 7/24
B. 5/12
C. 7/17
D. 5/17
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

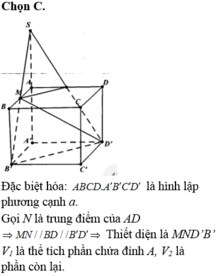
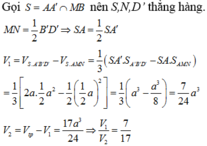

Đáp án B
Dựng MN//BD//B'D'
Chia thể tích khối A'B'D'.AMN thành 3 khối chóp
Ta có: V A ' B ' D ' . A M N = V N . A ' B ' D ' + V N . A ' B ' M ' + V A ' . A M N
= 1 2 V N . A ' B ' C ' D ' + 1 2 V D . A ' B ' M + 1 4 V A ' . A B D
= 1 6 V + 1 2 V D ' . A ' B ' M + 1 24 V = 1 6 V + 1 12 V + 1 24 V = 7 24 V
Do đó tỷ số thể tích 2 phần là V 1 V 2 = 7 17

Chọn đáp án C.

là đường thẳng đi qua M, song song với AC và cắt BC tại trung điểm N của cạnh BC.
Gọi h là độ dài chiều cao của hình hộp đã cho. Khi đó:
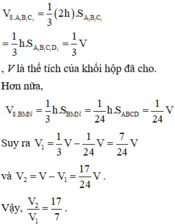

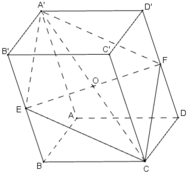
Gọi O là tâm hình hộp và tâm của hình bình hành BB’D’D. Khi đó O là trung điểm của EF.
Ta có: A’ ∈ CO (1)
CO ⊂ mp(CEF)(2)
Mặt khác A’E // CF, A’F // CE
Nên mp(CEF) cắt hình hộp theo thiết diện là hình bình hành A’ECF.
mp(CEF) chia hình hộp ABCD.A’B’C’D’ thành hai khối đa diện (Đ) và (Đ’).
Gọi (Đ) là khối đa diện có các đỉnh là A, B, C, D, A’, E, F và (Đ’) là khối đa diện còn lại.
Phép đối xứng qua tâm O biến các đỉnh A, B, C, D, A’, E, F của đa diện (Đ) lần lượt thành các đỉnh C’, D’, A’, B’, C, F, E của khối da diện (Đ’)
Suy ra phép đối xứng qua tâm O biến (Đ) thành (Đ’), nghĩa là hai hình đa diện (Đ) và (Đ’) bằng nhau.
Vậy tỉ số thể tích của (Đ) và (Đ’) bằng 1.