Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a, gọi φ là góc giữa hai mặt phẳng S A B v à C S D . Tính c...

PT

Pham Trong Bach

6 tháng 4 2017

Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a, gọi φ là góc giữa hai mặt phẳng S A B v à C S D . Tính cos φ A. cos φ = 1 2 B. cos φ = 1 6 C. cos φ = 1 3 D. cos φ = 1 4 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

6 tháng 4 2017

Đáp án C

Đúng(0)

PT

Pham Trong Bach

22 tháng 4 2019

Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a, gọi φ là góc giữa hai mặt phẳng (SAB) và (CSD) Tính cos φ A. cos φ = 1 2 B. cos φ = 1 6 C. cos φ = 1 3 D. cos φ = 1 4 ...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

22 tháng 4 2019

Đáp án C

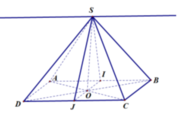
Giao tuyến giữa (SAB) và (CSD) là đường thằng d qua S và song song AB, CD. Gọi I, J theo thứ tự là trung điểm AB, CD

Suy ra SI, SJ cùng vuông góc với d tại S.

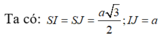
Áp dụng định lý cosin trong tam giác ISJ:

Đúng(0)

NT

Nguyễn Thùy Chi

17 tháng 7 2023

Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Gọi E là trung điểm cạnh S. Tính cosin của góc giữa hai mặt phẳng (SBD) và...

Đọc tiếp

#Toán lớp 11

0

PT

Pham Trong Bach

2 tháng 8 2019

Cho hình chóp tứ giác đều S.ABCD, có cạnh đáy bằng a và có thể tích V = a 3 3 6 Gọi J là điểm cách đều tất cả các mặt của hình chóp. Tính khoảng cách d từ J đến mặt phẳng đáy. A. d = a 3 4 B. d = a 3 2 C. d = a 3 6 D. d = a 3 3 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

2 tháng 8 2019

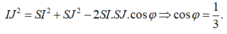
Đáp án là C.

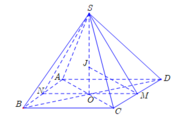
Gọi O là tâm hình vuông ABCD .Ta có đường cao của hình chóp SABCD là SO

V S A B C D = 1 3 S 0 . S A B C D ⇔ 3 6 a 8 = 1 3 S O . a 2 ⇒ S O = 3 2 a .

Xét tam giác SMO ta có SM= S 0 2 + O M 2 = ( 3 2 a ) 2 + ( a 2 ) 2 = a

Gọi M,N lần lượt là trung điểm của AB,CD.Khi đó J là tâm đường tròn nội tiếp tam giác SMN. Khi đó ta có MJ là đường phân giác của tam giác SMN.

Suy ra : S J J O = M S M O = a a = 2 ⇒ S J = 2 J O .

Mà S 0 = S J + J O = 3 2 a ⇔ 3 J O = 3 2 a ⇔ J O = 3 6

Đúng(0)

PT

Pham Trong Bach

29 tháng 5 2019

Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Côsin góc giữa hai mặt phẳng (SAB) và (SAD) bằng ...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

29 tháng 5 2019

ĐÁP ÁN: B

Đúng(0)

PT

Pham Trong Bach

18 tháng 8 2018

Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Côsin góc giữa hai mặt phẳng (SAB) và (SAD) bằng

A. 3 4

B. 1 3

C. 1 4

D. 2 3

#Mẫu giáo

1

CM

Cao Minh Tâm

18 tháng 8 2018

Đúng(0)

PT

Pham Trong Bach

5 tháng 2 2018

Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a Gọi M là điểm trên đoạn SD sao cho SM=2MD Tính tan góc giữa đường thẳng BM và mặt phẳng (ABCD)

A . 1 3

B . 5 5

C . 3 3

D . 1 5

#Mẫu giáo

1

CM

Cao Minh Tâm

5 tháng 2 2018

Đúng(0)

B

Buddy

20 tháng 8 2023

Cho hình chóp tứ giác đều \(S.ABCD\) với \(O\) là tâm của đáy và có tất cả các cạnh đều bằng \(a\). Xác định và tính góc phẳng nhị diện:

a) \(\left[ {S,BC,O} \right]\);

b) \(\left[ {C,SO,B} \right]\).

#Toán lớp 11

1

H

HaNa

20 tháng 8 2023

a) `[S,BC,O]`:

Góc phẳng nhị diện `[S,BC,O`] là góc giữa mặt phẳng `(SBC)` và mặt phẳng `(SBO)`. Vì hình chóp tứ giác đều, nên mặt phẳng `(SBC)` và mặt phẳng `(SBO)` là hai mặt phẳng vuông góc với nhau. Do đó, góc phẳng nhị diện `[S,BC,O]` là góc vuông.

b) `[C,SO,B]`:
Góc phẳng nhị diện `[C,SO,B]` là góc giữa mặt phẳng `(CSO)` và mặt phẳng `(CSB)`. Vì hình chóp tứ giác đều, nên mặt phẳng `(CSO)` và mặt phẳng `(CSB)` là hai mặt phẳng vuông góc với nhau. Do đó, góc phẳng nhị diện` [C,SO,B]` là góc vuông.

Đúng(2)

PT

Pham Trong Bach

13 tháng 2 2017

Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi M là trung điểm của SD. Tang của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng

A. 1 3

B. 2 2

C. 3 3

D. 2 3

#Mẫu giáo

1

CM

Cao Minh Tâm

13 tháng 2 2017

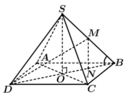
Gọi O là tâm hình vuông, suy ra

Trong tam giác vuông SOB tính được

Gọi N là trung điểm OD, suy ra MN//SO nên Khi đó

Xét tam giác vuông BNM ta có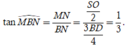

Chọn A.

Đúng(0)

NV

nguyễn văn linh

7 tháng 5 2023

Cho hình chóp đều tứ giác đều S ABCD . có tất cả các cạnh bằng a . Gọi O là giao điểm AC và BD
a) Chứng minh SA vuông góc với SC.

b) Tính góc giữa mặt bên và mặt đáy.

c) Tính khoảng cách từ A đến mặt phẳng (SCD)

#Toán lớp 11

2

NV

Nguyễn Việt Lâm

Giáo viên

7 tháng 5 2023

a.

\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)

\(SA=SC=a\Rightarrow SA^2+SC^2=AC^2\)

\(\Rightarrow\Delta SAC\) vuông tại S (Pitago đảo)

\(\Rightarrow SA\perp SC\)

b.

Gọi E là trung điểm CD \(\Rightarrow OE\perp CD\)

Chóp tứ giác đều \(\Rightarrow SO\perp\left(ABCD\right)\Rightarrow SO\perp CD\)

\(\Rightarrow CD\perp\left(SOE\right)\)

Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\Rightarrow\widehat{SEO}\) là góc giữa mặt bên và đáy

\(OE=\dfrac{1}{2}BC=\dfrac{a}{2}\) (đường trung bình) ; \(SO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\) (trung tuyến ứng với cạnh huyền)

\(\Rightarrow tan\widehat{SEO}=\dfrac{SO}{OE}=\sqrt{2}\Rightarrow\widehat{SEO}=...\)

c.

Từ O kẻ \(OF\perp SE\Rightarrow OF\perp\left(SCD\right)\)

\(\Rightarrow OF=d\left(O;\left(SCD\right)\right)\)

Hệ thức lượng trong tam giác vuông SOE:

\(\dfrac{1}{OF^2}=\dfrac{1}{SO^2}+\dfrac{1}{OE^2}\Rightarrow OF=\dfrac{SO.OE}{\sqrt{SO^2+OE^2}}=\dfrac{a\sqrt{6}}{6}\)

\(\left\{{}\begin{matrix}AO\cap\left(SCD\right)=C\\AC=2OC\end{matrix}\right.\) \(\Rightarrow d\left(A;\left(SCD\right)\right)=2d\left(O;\left(SCD\right)\right)=2OF=\dfrac{a\sqrt{6}}{3}\)

Đúng(2)

NV

Nguyễn Việt Lâm

Giáo viên

7 tháng 5 2023

loading...

Đúng(1)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP