Mn giúp em với ạ em đang cần gấp ạ 🥺😭
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 6 2021
a) Vì ABCD là hình bình hành ( gt )
⇒ AD // BC
F ∈ BC
⇒ AD // BF
⇒ ∠EDA = ∠EFB ( hai góc so le trong )
Xét △AED và △BEF, có :
∠EDA = ∠EFB ( cmt )
∠AED = ∠FEB ( hai góc đối đỉnh )
⇒ △AED ∼ △BEF (g-g)
b) Vì ABCD là hình bình hành ( gt )
⇒ AB // CD
E ∈ AB
⇒ BE // CD
Xét △FDC, có :
BE // CD ( cmt )
E ∈ DF ; B ∈ DC
⇒ \(\dfrac{FB}{FC}=\dfrac{EB}{DC}\) (Hệ quả của định lí Ta-let)
⇒ \(\dfrac{BF}{BE}=\dfrac{FC}{DC}\) (1)
Vì △AED ∼ △BEF ( cmt )
⇒ \(\dfrac{AE}{BE}=\dfrac{AD}{BF}\) (TSDD)
⇒ \(\dfrac{AE}{AD}=\dfrac{BE}{BF}\) (2)
Từ (1) và (2) ⇒ \(\dfrac{AE}{AD}=\dfrac{CF}{CD}\)
⇒ AD.CD = AE.CF
c) Xét △DGC, có :
AE // DC ( cmt )
G ∈ AC ; G ∈ DE
⇒ \(\dfrac{DG}{DE}=\dfrac{GC}{AC}\) (Hệ quả của định lí Ta-let) (3)
Xét △FGC, có :
AD // CF ( cmt )
G ∈ AC ; G ∈ DF
⇒ \(\dfrac{DG}{DF}=\dfrac{AG}{AC}\) (Hệ quả của định lí Ta-let) (4)
Từ (3) và (4) ⇒ \(\dfrac{DG}{DE}+\dfrac{DG}{DF}=\dfrac{GC}{AC}+\dfrac{AG}{AC}\)
⇒ \(\dfrac{DG}{DE}+\dfrac{DG}{DF}\) = 1
⇒ \(\dfrac{1}{DG}\left(\dfrac{DG}{DE}+\dfrac{DG}{DF}\right)=\dfrac{1}{DG}\)
⇒ \(\dfrac{1}{DG}=\dfrac{1}{DE}+\dfrac{1}{DF}\)
17 tháng 1 2022
a: 2+5/6=12/6+5/6=17/6
b: 5/12+3/4+1/3=5/12+9/12+4/12=18/12=3/2
c: 2/3+3/4=8/12+9/12=17/12
21 tháng 12 2021
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔBAC
18 tháng 12 2021
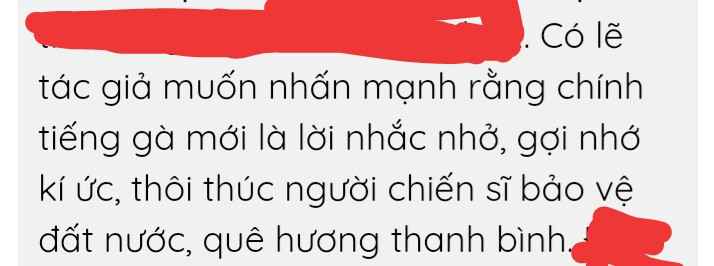
Tác giả muốn nhấn mạnh rằng chính tiếng gà mới là lời nhắc nhở, gợi nhớ kí ức, thôi thúc người chiến sĩ bảo vệ đất nước, quê hương thanh bình.