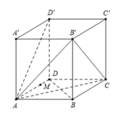
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = 2a, AD = 4a. Gọi M là trung điểm của cạnh AD. Tính khoảng cách d từ giữa hai đường thẳng A’B’ và C’M.
A. d = 2 a 2
B. d = a 2
C. d = 2a
D. d = 3a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Chọn hệ trục tọa độ như hình vẽ
A'(0;0;0), B'(4a;0;0), C'(4a;4a;0), M'(0;2a;2a)
A ' B ' → 4 a ; 0 ; 0 , C ' M → - 4 a ; - 2 a ; 2 a ⇒ A ' B ' → , C ' M → = 0 ; - 8 a 2 ; - 8 a 2 A ' M → 0 ; 2 a ; 2 a d ( A ' B ' , C ' M ) = A ' B ' → , C ' M → A ' M A ' B ' → , C ' M → = 32 a 3 8 2 a 2 = 2 2 a
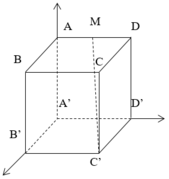

Đáp án A
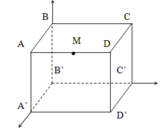
Giả sử AB = x
B ' ( 0 ; 0 ; 0 ) , A ' ( x ; 0 ; 0 ) , C ' ( 0 ; 4 a ; 0 ) , M ( x ; 2 a ; 2 a ) A ' B ' → ( x ; 0 ; 0 ) , C ' M → ( x ; − 2 a ; 2 a ) , B ' C ' → ( 0 ; 4 a ; 0 ) [ A ' B ' → , C ' M → ] = ( 0 ; − 2 a x ; − 2 a x ) d ( A ' B ' ; C ' M ) = [ A ' B ' → , C ' M → ] B ' C ' → [ A ' B ' → , C ' M → ] = − 8 a 2 x 8 a 2 x 2 = 2 2 a

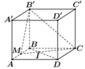
Khoảng cách từ D đến (B'MC)
gấp hai lần khoảng cách từ B đến (B'MC)
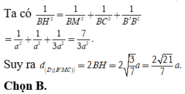

Đáp án B
Ta có d D ; A B ' C = d B ; A B ' C mà A M A D = 3 4
Và 1 d 2 B ; A B ' C = 1 A B 2 + 1 B C 2 + 1 B B ' ⇒ d M ; A B ' C = a 2 .
Gọi E, F lần lượt là trung điểm của AD’, B’C.
Suy ra EF là đoạn vuông góc chung cuả AD’, B’C.
Do đó d A D ' ; B ' C = E F = A B = a . Vậy x y = a . a 2 = a 2 2 .
Đáp án A
Chọn hệ trục tọa độ như hình vẽ
A ' ( 0 ; 0 ; 0 ) , B ' ( 4 a ; 0 ; 0 ) , C ' ( 4 a ; 4 a ; 0 ) , M ( 0 ; 2 a ; 2 a ) A ' B ' → ( 4 a ; 0 ; 0 ) , C ' M → ( − 4 a ; − 2 a ; 2 a ) ⇒ [ A ' B ' → , C ' M → ] = ( 0 ; − 8 a 2 ; − 8 a 2 ) A ' M → ( 0 ; 2 a ; 2 a ) d ( A ' B ' , C ' M ) = [ A ' B ' → , C ' M → ] A ' M → [ A ' B ' → , C ' M → ] = 32 a 3 8 2 a 2 = 2 2 a