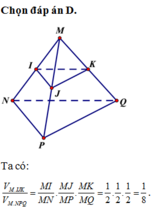
Cho tứ diện MNPQ. Gọi I

PT

Pham Trong Bach

24 tháng 6 2018

Cho tứ diện MNPQ. Gọi I ; J ; K lần lượt là trung điểm của các cạnh M N ; M P ; M Q . Tỉ số thể tích V M I J K V M N P Q bằng A. 1 3 B. 1 4 C. 1 6 D. 1 8 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

24 tháng 6 2018

Đúng(0)

PT

Pham Trong Bach

29 tháng 11 2019

Cho tứ diện MNPQ. Gọi I;J;K lần lượt là trung điểm các cạnh MN;MP;MQ. Tỉ số thể tích V M I J K V M N P Q bằng

A. 1 4

B. 1 3

C. 1 8

D. 1 6

#Mẫu giáo

1

CM

Cao Minh Tâm

29 tháng 11 2019

Đúng(0)

PT

Pham Trong Bach

10 tháng 5 2018

Cho tứ diện MNPQ. Gọi I, J, K lần lượt là trung điểm các cạnh MN, MP, MQ. Tỉ số thể tích V M I J K V M N P Q bằng: A. 1 4 B. 1 3 C. 1 8 D. 1 6 ...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

10 tháng 5 2018

Chọn C.

Đúng(0)

LP

Lê Phong

12 tháng 1 2022

Cho tứ giác MNPQ. Gọi H, I, J, K lần lượt là trung điểm của MN, MP, PQ, QN. Tứ giác HKJI là hình gì? Vì sao? Tìm điều kiện để tứ giác MNPQ và tứ giác HKJI là hình thoiCho tứ giác MNPQ. Gọi H,I,J,K lần lượt là trung điểm của MN, MP,PQ,QNa) Tứ giác HKJI là hình gì ? Vì saob) Tìm điều kiện để tứ giác MNPQ và tứ giác HKJI là hình...

Đọc tiếp

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

12 tháng 1 2022

a: Xét ΔMNP có

H là trung điểm của MN

I là trung điểm của MP

Do đó: HI là đường trung bình

=>HI//NP và HI=NP/2(1)

Xét ΔPQN có

J là trung điểm của PQ

K là trung điểm của QN

Do đó: JK là đường trung bình

=>JK//PN và JK=PN/2(2)

Từ (1) và (2) suy ra HI//KJ và HI=KJ

hay HKJI là hình bình hành

b: Để HKJI là hình thoi thì HJ⊥KI

hay MP⊥NQ

Đúng(0)

NT

Nguyễn Thị Phương Thảo

21 tháng 1 2020 - olm

Cho hình bình hành MNPQ. Gọi X là trung điểm của PQ, I là trung điểm NP. Biết diện tích hình bình hành bằng 30cm2. Tìm diện tích tứ giác MXPI

#Toán lớp 8

0

PT

Pham Trong Bach

24 tháng 8 2017

Cho tứ diện ABCD có thể tích 9 3 c m 3 . Gọi M, N, P, Q lần lượt là trọng tâm các mặt của khối tứ diện ABCD . Thể tích khối tứ diện MNPQ là A. 2 3 3 c m 3 B. 3 3 c m 3 C. 3 3 c m 3 D. 3 c m 3 ...

Đọc tiếp

#Mẫu giáo

2

CM

Cao Minh Tâm

24 tháng 8 2017

Đáp án B

Ta có:

V M N P Q V A B C D = 1 3 . 1 3 2 = 1 27 ⇒ V M N P Q = V A B C D 27 = 9 3 27 = 3 3 c m 3

Đúng(0)

LT

Lưu Thị Bảo Trâm

VIP

7 tháng 3

n

Đúng(0)

TT

Trần thị thùy trang

30 tháng 12 2021

Cho tứ giác ABCD gọi M ,N ,P, Q lần lượt là trung điểm của AB ,BC ,CD, DA a) Chứng minh tứ giác MNPQ là hình chữ nhật b) tính diện tích tứ giác MNPQ biết AC = 12 cm ,BC = 10 cm

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

30 tháng 12 2021

a: Xét ΔABD có

M là trung điểm của AB

Q là trung điểm của AD

Do đó: MQ là đường trung bình

=>MQ//BD và MQ=BD/2(1)

Xét ΔBCD có

N là trung điểm của BC

P là trung điểm của CD

Do đó: NP là đường trung bình

=>NP//BD và NP=BD/2(2)

Từ (1) và (2) suy ra MQ//NP và MQ=NP

hay MQPN là hình bình hành

Đúng(0)

HN

Huỳnh Ngân

27 tháng 3 2020

Bài 22. Cho hình thang cân ABCD với AB // CD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA.

a) Tứ giác MNPQ là hình gì?

b) Cho biết diện tích tứ giác ABCD bằng 60cm². Tính diện tích tứ giác MNPQ.

#Toán lớp 8

0

P

PUBGM̃̃̃̃̃̃̃̃̉̃̉̃̃̃́̃̃̃́̃́̃̀̉́́́́́́...

3 tháng 7 2021

Cho tứ giác ABCD. Gọi M,N,P,Q lần lượt là trung điểm của AB,BC,CD,DA.
a) Tứ giác MNPQ là hình gì? Vì sao?
b) Tìm điều kiện của tứ giác ABCD để tứ giác MNPQ là hình vuông?
c) Với điều kiện câu b) hãy tính tỉ số diện tích của tứ giác ABCD và MNPQ

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

3 tháng 7 2021

a) Xét ΔABC có

M là trung điểm của AB(gt)

N là trung điểm của BC(gt)

Do đó: MN là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)

Suy ra: MN//AC và \(MN=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(1)

Xét ΔADC có

Q là trung điểm của AD(gt)

P là trung điểm của CD(gt)

Do đó: QP là đường trung bình của ΔADC(Định nghĩa đường trung bình của tam giác)

Suy ra: QP//AC và \(QP=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(2)

Từ (1) và (2) suy ra MN//PQ và MN=PQ

Xét tứ giác MNPQ có

MN//PQ(cmt)

MN=PQ(cmt)

Do đó: MNPQ là hình bình hành(Dấu hiệu nhận biết hình bình hành)

b)

Xét ΔABD có

M là trung điểm của AB(gt)

Q là trung điểm của AD(gt)

Do đó: MQ là đường trung bình của ΔADB(Định nghĩa đường trung bình của tam giác)

Suy ra: \(MQ=\dfrac{BD}{2}\)(Định lí 2 về đường trung bình của tam giác)

Hình bình hành MNPQ trở thành hình vuông khi \(\left\{{}\begin{matrix}\widehat{MQP}=90^0\\MQ=QP\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}AB\perp CD\\AB=CD\end{matrix}\right.\)

Hình bình hành MNPQ trở thành hình vuông khi

Đúng(2)

SA

shinzo abe

22 tháng 2 2017 - olm

cho hình tứ giác ABCD có diện tích bằng 90m2.Gọi M:N:P:Q lần lượt là trung điểm của AB:BC:CD:DA.Nối MN:NP:PQ và QM.Tính diện tích tứ giác MNPQ.

#Toán lớp 5

2

V

VuiLaChinh

22 tháng 2 2017

S(MNPQ) = 1/2 S(ABCD)

DT tứ giác NMPQ :

90 : 2 = 45 m²

Đúng(0)

SA

shinzo abe

23 tháng 2 2017

bạn có chắc ko zậy

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP