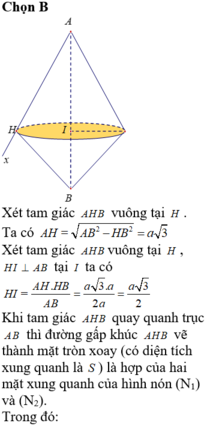
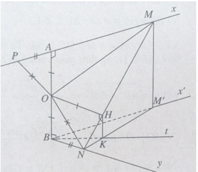
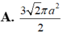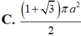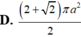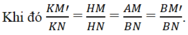Cho đoạn thẳng AB có độ dài bằng 2a, vẽ tia Ax về phía điểm B sao cho điểm B luôn cách tia Ax một đoạn bằng a. Gọi H là hình chiếu của B lên tia Ax, khi tam giác AHB quay quanh trục AB thì đường gấp khúc AHB vẽ thành mặt tròn xoay có diện tích xung quanh bằng: