dạ giúp e câu 2 phần c (c/m DK // BC) e cho kẹo ạ :3
e vẽ hình luôn ròi nha


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b) Xét tam giác ABF có:
BH là đường cao(AH⊥BH)
BH là phân giác( BC là phân giác \(\widehat{ABF}\))
=> Tam giác ABF cân tại B
=> AB=BF
Mà AB=CE(ΔMBA=ΔMCE)
=> CE=BF
c) Ta có: \(\widehat{ABC}=\widehat{BCE}\left(\Delta MBA=\Delta MCE\right)\)
Mà \(\widehat{ABC}=\widehat{KBC}\)(BC là phân giác \(\widehat{ABF}\))
\(\Rightarrow\widehat{BCE}=\widehat{KBC}\)
=> Tam giác KBC cân tại K
=> KM là đường trung tuyến cũng là đường phân giác \(\widehat{BKC}\left(1\right)\)
Ta có: KB=KC(KBC cân tại K), BF=CD(cmt)
=> KB-BF=KC-CE=> KF=KE
Xét tam giác BEK và tam giác CFK có:
KF=KE(cmt)
\(\widehat{K}\) chung
BK=KB(KBC cân tại K)
=> ΔBEK=ΔCFK(c.g.c)
=> \(\widehat{EBK}=\widehat{KCF}\)
Xét tam giác BFC và tam giác CEB có:
BC chung
\(\widehat{FBC}=\widehat{BCE}\)(cmt)
BF=CE(cmt)
=> ΔBFC=ΔCEB(c.g.c)
=> \(\widehat{BFC}=\widehat{BEC}\)
Xét tam giác BFI và tam giác CEI có:
\(\widehat{BFC}=\widehat{BEC}\left(cmt\right)\)
BF=CE(cmt)
\(\widehat{FBI}=\widehat{ECI}\left(cmt\right)\)
=> ΔBFI=ΔCEI(g.c.g)
=> IF=IC
=> ΔIFK=ΔIEK(c.c.c)
=> KI là phân giác \(\widehat{BKC}\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow M,I,K\) thẳng hàng

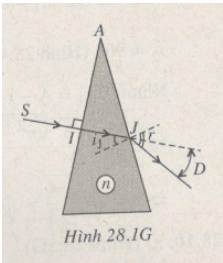
Câu 9.
Tại điểm \(I\): \(i=r=0\)
Tia sáng truyền thẳng vào lăng kính.
Tại điểm J có \(i_J=30^o\)
Theo định luật khúc xạ ánh sáng:
\(sinr=nsini_J=1,5\cdot sin30^o=\dfrac{3}{4}\Rightarrow r=arcsin\dfrac{3}{4}\)
Góc lệch:
\(D=r-i_J=arcsin\dfrac{3}{4}-30^o\approx18,6^o\)
Chọn B.
Hình vẽ tham khảo sgk lí 11!!!

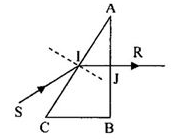
Theo đinh luật khúc xạ ánh sáng (tại điểm \(I\)) :
\(sini_1=nsinr_1\)
\(\Rightarrow sin45^o=\sqrt{2}\cdot sinr_1\Rightarrow sinr_1=\dfrac{1}{2}\Rightarrow r_1=30^o\)
Tam giác ABC đều\(\Rightarrow\)Góc chiết quang \(\widehat{A}=60^o=r_1+r_2\)
\(\Rightarrow r_2=30^o\)
Xét tại điểm J, theo định luật khúc xạ ánh sáng:
\(sini_2=nsinr_2=\sqrt{2}\cdot sin30^o=\dfrac{\sqrt{2}}{2}\Rightarrow i_2=45^o\)
Góc lệch tia ló ra khỏi lăng kính so với tia tới:
\(D=i_1+i_2-A=45^o+45^o-60^o=30^o\)
Chọn A

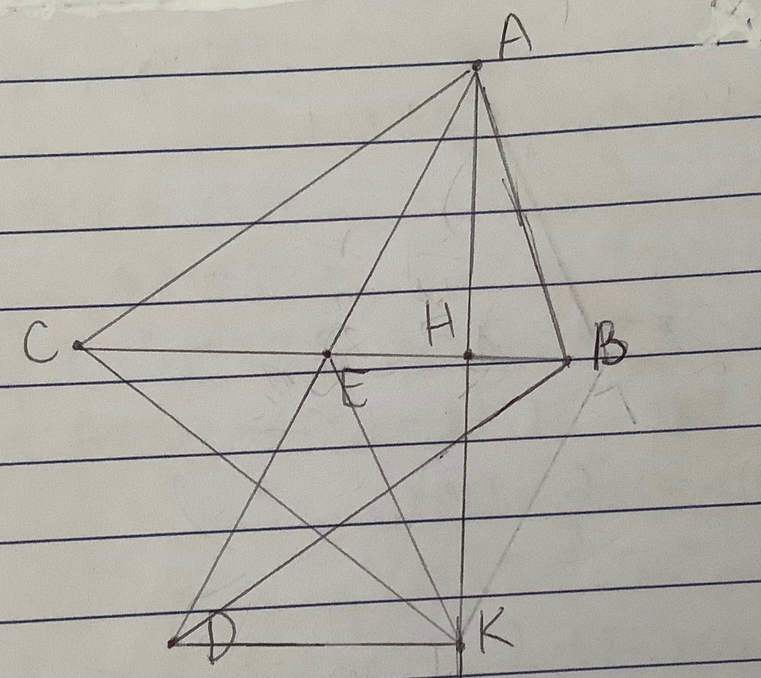
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
Hình bình hành ABDC có \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
b: Xét ΔMHA vuông tại H và ΔMKD vuông tại K có
MA=MD
\(\widehat{HMA}=\widehat{KMD}\)(hai góc đối đỉnh)
Do đó: ΔMHA=ΔMKD
=>MH=MK
=>M là trung điểm của HK
Xét tứ giác AHDK có
M là trung điểm chung của AD và HK
=>AHDK là hình bình hành

Để chứng minh a là trung điểm của HK, ta cần chứng minh rằng a là trung điểm của HK.
Gọi a là trung điểm của HK, ta cần chứng minh rằng HA = AK.
Ta có:
- Tam giác ABC là tam giác cân tại A, nên AH là đường cao của tam giác ABC và cắt BC thành hai phần bằng nhau. Vậy H là trung điểm của BC.
- Ta biết MN là đường thẳng vuông góc với BC, nên HK là đường cao của tam giác MNK và cắt MN thành hai phần bằng nhau. Vậy K là trung điểm của MN.
Vậy ta có AH = HK và AK là đường trung bình của tam giác AMN.
Ta cần chứng minh AK = HA.
Gọi P là giao điểm của AK và HA.
Ta có:
- Ta biết AH = HK, nên tam giác AHK là tam giác cân tại H. Vậy góc AHK = góc AKH.
- Ta biết MN là đường thẳng vuông góc với BC, nên tam giác MNK là tam giác vuông tại K. Vậy góc MNK = 90 độ.
- Ta biết AK là đường trung bình của tam giác AMN, nên góc AKH = góc MNK.
Từ các quan sát trên, ta có:
góc AHK = góc AKH = góc MNK = 90 độ.
Vậy tứ giác AKHG là hình chữ nhật với AK = HG.
Vậy ta đã chứng minh được a là trung điểm của HK.

a: Xét tứ giác AMKN có
\(\widehat{AMK}=\widehat{ANK}=\widehat{MAN}=90^0\)
=>AMKN là hình chữ nhật
b: Xét ΔABC có
K là trung điểm của BC
KM//AC
Do đó: M là trung điểm của AB
Xét ΔABC có
K là trung điểm của BC
KN//AB
Do đó: N là trung điểm của AC
Xét tứ giác AKBE có
M là trung điểm chung của AB và KE
nên AKBE là hình bình hành
Xét hình bình hành AKBE có AB\(\perp\)KE
nên AKBE là hình thoi
c: Xét tứ giác AKCF có
N là trung điểm chung của AC và KF
nên AKCF là hình bình hành
=>CF//AK và CF=AK
AKBE là hình bình hành
=>BE//AK và BE=AK
BE//AK
CF//AK
Do đó: BE=CF
BE=AK
CF=AK
Do đó: BE=CF
Ta có:\(AH=HK\left(gt\right);AE=ED\left(gt\right)\Rightarrow\)EH là đường trung bình trong tam giác AKD⇒EH//DK⇒BC//DK
🍬