Cho vật thể H nằm giữa hai mặt phẳng x=0;x=1. Biết rằng thiết diện của vật thể H cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x( 0 ≤ x ≤ 1 ) là một tam giác đều có cạnh là 4 ln ( 1 + x ) Giả sử thể tích V của vật thể có kết quả là V = a b ( c ln 2 - 1 ) với a, b, c là các số nguyên. Tính tổng S= a 2 - a b + c
![]()
![]()
![]()
![]()


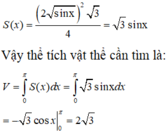

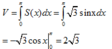

Đáp án B.