Giá trị m để đồ thị hàm số
y
=
x
+
1
x
2
-
2
x
+
m
có 3 đường tiệm cận. ...
Đọc tiếp
Giá trị m để đồ thị hàm số y = x + 1 x 2 - 2 x + m có 3 đường tiệm cận.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 1
a: \(\lim\limits_{x\rightarrow-\dfrac{3m}{2}}\dfrac{x+3}{2x+3m}=\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-\dfrac{3m}{2}}2x+3m=0\\\lim\limits_{x\rightarrow-\dfrac{3m}{2}}x+3=\dfrac{-3m}{2}+3\end{matrix}\right.\)
=>x=-3m/2 là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{x+3}{2x+3m}\)
Để tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x+3}{2x+3m}\) đi qua M(3;-1) thì \(-\dfrac{3m}{2}=3\)
=>-1,5m=3
=>m=-2
b: \(\lim\limits_{x\rightarrow-m}\dfrac{2x-3}{x+m}=\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-m}2x-3=-2m-3\\\lim\limits_{x\rightarrow-m}x+m=0\end{matrix}\right.\)
=>x=-m là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{2x-3}{x+m}\)
Để x=-2 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{2x-3}{x+m}\) thì -m=-2
=>m=2
c: \(\lim\limits_{x\rightarrow\dfrac{2}{b}}\dfrac{ax+1}{bx-2}=\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow\dfrac{2}{b}}ax+1=a\cdot\dfrac{2}{b}+1\\\lim\limits_{x\rightarrow\dfrac{2}{b}}bx-2=b\cdot\dfrac{2}{b}-2=0\end{matrix}\right.\)
=>Đường thẳng \(x=\dfrac{2}{b}\) là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{ax+1}{bx-2}\)
=>2/b=2
=>b=1
=>\(y=\dfrac{ax+1}{x-2}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{ax+1}{x-2}=\lim\limits_{x\rightarrow+\infty}\dfrac{a+\dfrac{1}{x}}{1-\dfrac{2}{x}}=a\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{ax+1}{x-2}=\lim\limits_{x\rightarrow-\infty}\dfrac{a+\dfrac{1}{x}}{1-\dfrac{2}{x}}=a\)
=>Đường thẳng y=a là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{ax+1}{x-2}\)
=>a=3
CM
29 tháng 3 2019
y = x + 1 - x 2 + 3 x x 2 + ( m + 1 ) x - m - 2 = ( x + 1 ) 2 - ( x 2 + 3 x ) ( x + 1 + x 2 + 3 x ) ( x - 1 ) ( x + m + 2 ) = - 1 ( x + 1 + x 2 + 3 x ) ( x + m + 2 )
+ Vì bậc tử số < bậc mẫu số nên luôn có một tiệm cận ngang y= 0
+ Vì phương trình x + 1 + x 2 + 3 x = 0 vô nghiệm nên chỉ có duy nhất một tiệm cận đứng nữa đó là đường thẳng x= -m-2.
Vậy với mọi x; đồ thị hàm số đã cho luôn có hai tiệm cận.
Chọn C.
CM
11 tháng 4 2018
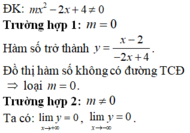
Suy ra đồ thị hàm số có 1 đường TCN y = 0.
Do đó đồ thị hàm số có đúng 2 đường tiệm cận đồ thị hàm số có đứng 1 đường tiệm cận đứng phương trình m x 2 - 2 x + 4 = 0 có nghiệm kép hoặc có 2 nghiệm phân biệt trong đó có 1 nghiệm x = 2.
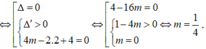
Vậy có 1 giá trị của m thỏa mãn yêu cầu bài toán.
Chọn A
.
.
CM
4 tháng 7 2018
Chọn D
Đồ thị hàm số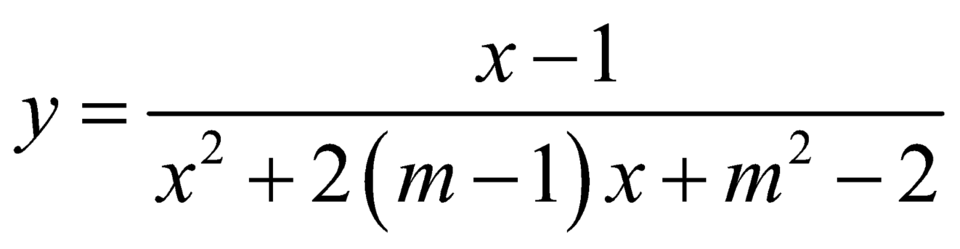 
có đúng hai tiệm cận đứng
có 2 nghiệm phân biệt khác 1.
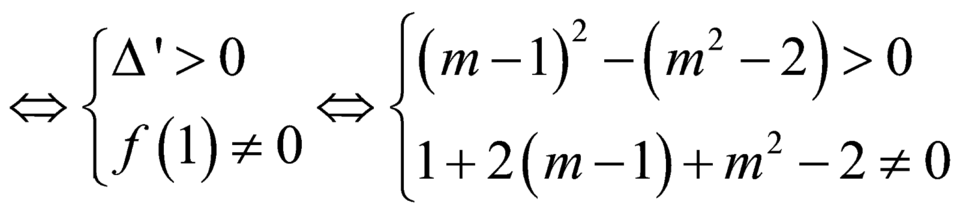
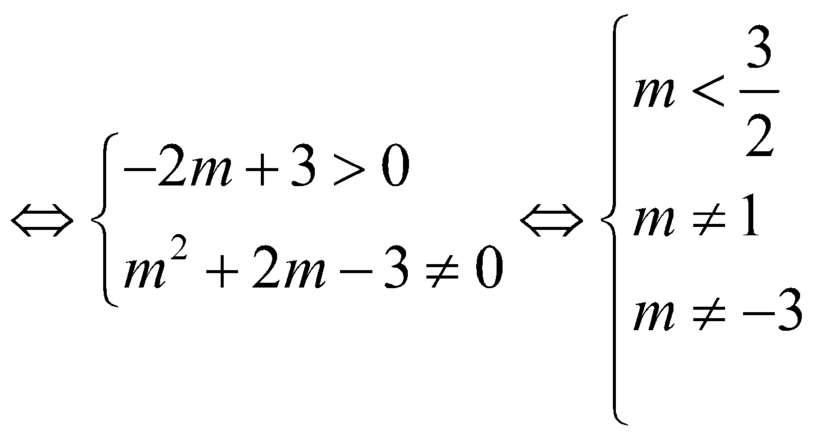
Chọn A