Cho dãy số u n xác định bởi u n = 1 n 2 3 n 2 . . . 2 n

PT

Pham Trong Bach

19 tháng 10 2018

Cho dãy số u n xác định bởi u n = 1 n 2 + 3 n 2 + . . . + 2 n - 1 n 2 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

19 tháng 10 2018

Đúng(0)

L

leducminh

28 tháng 1 2022 - olm

Cho dãy số (Un) xác định bởi U1=-3 và U(n+1)=Un+ n^2 -3n +4, mọi n thuộc N*. Số 1391 là số hạng thứ mấy của dãy ?

#Toán lớp 11

0

LT

Lê Trọng

29 tháng 12 2019 - olm

Cho dãy số xác định bởi u1=1 , u n+1 = \(2un+\frac{n-1}{n^2+3n+2}\). khi đó u 2018 bằng

#Toán lớp 11

0

NA

Nguyễn Anh Dũng An

10 tháng 1 2022 - olm

Cho dãy số được xác định bởi: U₁=12

\(\frac{2\cdot U_{n+1}}{n^2+5n+6}=\frac{U_n+n^2-n-2}{n^2+n}\)

Tìm số hạng tổng quát của dãy số

#Toán lớp 11

0

PT

Pham Trong Bach

5 tháng 11 2017

Cho dãy số u ( n ) xác định bởi u ( 1 ) = 1 ; u ( m + n ) = ...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

5 tháng 11 2017

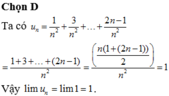
Chọn A

Phương pháp: Tìm công thức số hạng tổng quát

Cách giải: Ta có:

u ( 1 ) = 1

u ( 2 ) = u ( 1 ) + u ( 1 ) = 2 u ( 1 ) + 1

u ( 3 ) = u ( 2 ) + u ( 1 ) = 3 u ( 1 ) + 1 + 2

u ( 4 ) = u ( 3 ) + u ( 1 ) = 4 u ( 1 ) + 1 + 2 + 3

. . .

u ( 2017 ) = u ( 2016 ) + u ( 1 ) = 2017 u ( 1 ) + 1 + 2 + 3 . . . + 2016

⇒ u ( 2017 ) = 1 + 2 + 3 . . . + 2016 + 2017 = 2035153

Đúng(0)

T

TH

23 tháng 8 2016 - olm

cho dãy số U_n được xác định bởi: U₁ = 1 ; U₂= 2 ; U₃ = 3 ; U_n+3= 2U_n+2+ U_n+1 - U_n ( n thuộc N^*) . Tìm U₂₅? ( giải theo công thức trên máy tính casio dùm mình nhé)

#Toán lớp 8

0

LT

Lê Thu Hiền

9 tháng 8 2021

Cho dãy số (u_n) xác định bởi : u₁=1 ,\(u_{n+1}=\dfrac{3}{2}\left(u_n-\dfrac{n+4}{n^2+3n+2}\right)\)

Tìm công thức số hạng tổng quát u_n theo n

#Toán lớp 11

1

NV

Nguyễn Việt Lâm

Giáo viên

9 tháng 8 2021

\(u_{n+1}=\dfrac{3}{2}\left(u_n-\dfrac{n+4}{\left(n+1\right)\left(n+2\right)}\right)=\dfrac{3}{2}\left(u_n-\dfrac{3}{n+1}+\dfrac{2}{n+2}\right)\)

\(\Leftrightarrow u_{n+1}-\dfrac{3}{n+1+1}=\dfrac{3}{2}\left(u_n-\dfrac{3}{n+1}\right)\)

Đặt \(u_n-\dfrac{3}{n+1}=v_n\Rightarrow\left\{{}\begin{matrix}v_1=u_1-\dfrac{3}{2}=-\dfrac{1}{2}\\v_{n+1}=\dfrac{3}{2}v_n\end{matrix}\right.\)

\(\Rightarrow v_n\) là CSN với công bội \(\dfrac{3}{2}\)

\(\Rightarrow v_n=-\dfrac{1}{2}\left(\dfrac{3}{2}\right)^{n-1}\)

\(\Rightarrow u_n=-\dfrac{1}{2}\left(\dfrac{3}{2}\right)^{n-1}+\dfrac{3}{n+1}\)

Đúng(2)

LT

Lê Thị Mỹ Hằng

29 tháng 5 2017 - olm

Xét dãy ( U_n ) ; n = 1,2,3,.... xác định bởi U₀ = 2, U_n= 3U_n-1 + 2n³ - 9n² + 9n - 3

a) Lập quy trình tính U_n ?

b) Tính U₂₀

#Toán lớp 9

0

T

títtt

30 tháng 8 2023

1) cho dãy số (un)(��) được xác định bởi un=\(n^2-1\)�=3�−1a) Tính u1,u2,u3,u4b) 99 là số hạng thứ mấy của dãy2) cho dãy số (un)(��) được xác định bởi \(u_n=\dfrac{2n-1}{n+1}\)a) Tính u1,u2,u3,u4b) \(\dfrac{13}{7}\) là số hạng thứ mấy của...

Đọc tiếp

#Toán lớp 11

2

M

meme

30 tháng 8 2023

a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = n^2 - 1:

u1 = 1^2 - 1 = 0 u2 = 2^2 - 1 = 3 u3 = 3^2 - 1 = 8 u4 = 4^2 - 1 = 15

Vậy u1 = 0, u2 = 3, u3 = 8, u4 = 15.

b) Để tìm số hạng thứ mấy trong dãy có giá trị 99, ta giải phương trình n^2 - 1 = 99:

n^2 - 1 = 99 n^2 = 100 n = 10 hoặc n = -10

Vì số hạng của dãy phải là số tự nhiên nên ta chọn n = 10. Vậy số hạng thứ mấy có giá trị 99 là u10.

a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = (2n - 1)/(n + 1):

u1 = (21 - 1)/(1 + 1) = 1/2 u2 = (22 - 1)/(2 + 1) = 3/3 = 1 u3 = (23 - 1)/(3 + 1) = 5/4 u4 = (24 - 1)/(4 + 1) = 7/5

Vậy u1 = 1/2, u2 = 1, u3 = 5/4, u4 = 7/5.

b) Để tìm số hạng thứ mấy trong dãy có giá trị 137137, ta giải phương trình (2n - 1)/(n + 1) = 137137:

(2n - 1)/(n + 1) = 137137 2n - 1 = 137137(n + 1) 2n - 1 = 137137n + 137137 137135n = 137138 n = 1

Vậy số hạng thứ mấy có giá trị 137137 là u1.

Đúng(0)

NL

Nguyễn Lê Phước Thịnh

30 tháng 8 2023

loading...

Đúng(0)

BC

Big City Boy

27 tháng 11 2023

Cho dãy số (Un) xác định bởi \(U_n=\dfrac{an^2-1}{n^2+3}\) với \(n\ge1\). Tập hợp các giá trị của a để dãy số (Un) tăng là?

#Toán lớp 11

1

NL

Nguyễn Lê Phước Thịnh

29 tháng 11 2023

\(U_n=\dfrac{an^2-1}{n^2+3}\)

\(=\dfrac{an^2+3a-3a-1}{n^2+3}\)

\(=a+\dfrac{-3a-1}{n^2+3}\)

Để dãy này là dãy tăng thì \(U_{n+1}>U_n\)

=>\(a+\dfrac{-3a-1}{\left(n+1\right)^2+3}>a+\dfrac{-3a-1}{n^2+3}\)

=>\(\dfrac{-3a-1}{\left(n+1\right)^2+3}>\dfrac{-3a-1}{n^2+3}\)

=>\(\dfrac{3a+1}{\left(n+1\right)^2+3}< \dfrac{3a+1}{n^2+3}\)(1)

TH1: 3a+1>0

=>a>-1/3

(1)=>\(\dfrac{1}{\left(n+1\right)^2+3}< \dfrac{1}{n^2+3}\)

=>\(\left(n+1\right)^2+3>n^2+3\)

=>\(\left(n+1\right)^2>n^2\)

=>\(n^2+2n+1-n^2>0\)

=>\(2n+1>0\)(luôn đúng với mọi n>=1)

TH2: 3a+1<0

=>a<-1/3

(2) trở thành \(\dfrac{1}{\left(n+1\right)^2+3}>\dfrac{1}{n^2+3}\)

=>\(\left(n+1\right)^2+3< n^2+3\)

=>\(n^2+2n+1-n^2< 0\)

=>2n+1<0

=>2n<-1

=>\(n< -\dfrac{1}{2}\)(loại)

Vậy: \(a>-\dfrac{1}{3}\)

Đúng(1)

MT

Mai Thị Thúy

9 tháng 8 2021

Cho dãy số (u_n) xác định bởi : u₁=3 , \(u_{n+1}=\dfrac{2u_n+2}{3}\) Với mọi N thuộc N*

Tìm công thức số hạng tổng quát u_n theo n

#Toán lớp 11

1

NV

Nguyễn Việt Lâm

Giáo viên

9 tháng 8 2021

\(u_{n+1}=\dfrac{2}{3}u_n+\dfrac{2}{3}\Rightarrow u_{n+1}-2=\dfrac{2}{3}\left(u_n-2\right)\)

Đặt \(u_n-2=v_n\Rightarrow\left\{{}\begin{matrix}v_1=u_1-2=1\\v_{n+1}=\dfrac{2}{3}v_n\end{matrix}\right.\)

\(\Rightarrow v_n\) là CSN với công bội \(q=\dfrac{2}{3}\Rightarrow v_n=1.\left(\dfrac{2}{3}\right)^{n-1}=\left(\dfrac{2}{3}\right)^{n-1}\)

\(\Rightarrow u_n=v_n+2=\left(\dfrac{2}{3}\right)^{n-1}+2\)

Đúng(1)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP