Tìm giá trị của m để hàm số y = x + m(sinx + cosx + m ) luôn đồng biến trên R
A. - 2 2 ≤ m ≤ 2 2
B. 0 ≤ m ≤ 2 2
C. - 2 2 ≤ m ≤ 0
D. - 2 ≤ m ≤ 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có: ![]()
Hàm số đồng biến trên R khi ![]()
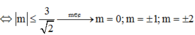
Vậy có 5 giá trị nguyên của m

Bài 1:
Để hàm số y=(2-m)x-2 là hàm số bậc nhất thì 2-m<>0
=>m<>2
a=2-m
b=-2
Bài 2:
a: Để hàm số y=(m-5)x+1 đồng biến trên R thì m-5>0
=>m>5
b: Để hàm số y=(m-5)x+1 nghịch biến trên R thì m-5<0
=>m<5
Bài 3:
a: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}3-m=2\\2\ne m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=1\\m\ne2\end{matrix}\right.\Leftrightarrow m=1\)
b: Để (d1) cắt (d2) thì \(3-m\ne2\)
=>\(m\ne1\)
c: Để (d1) cắt (d2) tại một điểm trên trục tung thì
\(\left\{{}\begin{matrix}3-m\ne2\\m=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne1\\m=2\end{matrix}\right.\)
=>m=2

Đạo hàm : y ' = 3 + m ( cos x - sin x ) = 3 + m 2 cos ( x + π 4 )
Hàm số đồng biến trên R khi y’ ≥ 0 với mọi x
⇔ M i n ℝ y ' ≥ 0 ⇔ 3 - m 2 ≥ 0 ⇔ m ≤ 3 2 → m ∈ ℤ m = 0 ; m = ± 1 ; m = ± 2 .
Vậy có 2 giá trị nguyên dương của m thỏa mãn đầu bài.
Chọn D.
y ' = 1 + m cos x - sin x = 1 - 2 m sin x - π 4
Đặt t = sin x - π 4 với t ∈ - 1 ; 1 ta có f 1 = 1 - 2 m t
Để hàm số đồng biến trên R thì
f t ≥ 0 ∀ t ∈ - 1 ; 1 ⇔ f - 1 ≥ 0 f 1 ≥ 0 ⇔ 1 + 2 m ≥ 0 1 - 2 m ≥ 0
⇔ m ≥ - 2 2 m ≤ 2 2 ⇔ - 2 2 ≤ m ≤ 2 2
Đáp án A