Phương trình
1 + 2 x + 1 - 2 a 2 - 1 x - 4 = 0 có 2 nghiệm phân biệt x 1 , x 2 thỏa mãn x 1 - x 2 = log 1 + 2 3 . Mệnh đề nào dưới đây đúng?


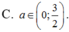
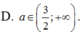
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét phương trình |x – 3| = 1
TH1: |x – 3| = x – 3 khi x – 3 ≥ 0 ó x ≥ 3
Phương trình đã cho trở thành x – 3 = 1 ó x = 4 (TM)
TH2: |x – 3| = 3 – x khi x – 3 < 0 ó x < 3
Phương trình đã cho trở thanh 3 – x = 1 ó x = 2 (TM)
Vậy phương trình |x – 3| = 1 có hai nghiệm x = 2 và x = 4 hay (1) sai và (3) đúng
|x – 1| = 0 ó x – 1 = 0 ó x = 1 nên phương trình |x – 1| = 0 có nghiệm duy nhất hay (2) sai.
Vậy có 1 khẳng định đúng
Đáp án cần chọn là: B

\(2x^2-4x-m=0\left(1\right)\)
a, Để pt (1) có hai nghiệm phân biệt thì Δ' > 0
\(\Rightarrow2+2m>0\Leftrightarrow m>-1\)
b, Theo viét : \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-\dfrac{m}{2}\end{matrix}\right.\)
Vì \(t_1,t_2\) là hai nghiệm của Phương trình \(x^2-Sx+P=0\) nên theo viét đảo có :
\(\left\{{}\begin{matrix}S=t_1+t_2=\dfrac{1}{x_1}+\dfrac{1}{x_2}\\P=t_1.t_2=\dfrac{1}{x_1x_2}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}S=\dfrac{x_1+x_2}{x_1x_2}\\P=\dfrac{1}{x_1x_2}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}S=\dfrac{2}{-\dfrac{m}{2}}\\P=\dfrac{1}{-\dfrac{m}{2}}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}S=-\dfrac{4}{m}\\P=-\dfrac{2}{m}\end{matrix}\right.\)
\(\Rightarrow\) Phương trình cần tìm là : \(x^2+\dfrac{4}{m}.x-\dfrac{2}{m}=0\) hay \(x^2m+4x-2=0\)

Đặt \(a=x^2\left(a>=0\right)\)
pt trở thành \(a^2+\left(1-2m\right)a+m^2-1=0\)
\(\text{Δ}=\left(1-2m\right)^2-4\left(m^2-1\right)\)
\(=4m^2-4m+1-4m^2+4=-4m+5\)
a: Để pt vô nghiệm thì -4m+5<0
hay m>5/4
b: Để phương trình có hai nghiệm phân biệt thì -4m+5>0
hay m<5/4
c: Để pt có 4 nghiệm phân biệt thì
\(\left\{{}\begin{matrix}m< \dfrac{5}{4}\\-2m+1>0\\m^2-1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{5}{4}\\m< \dfrac{1}{2}\\\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m< -1\\\dfrac{1}{2}< m< 1\end{matrix}\right.\)

a: x^2+2xm+m^2=0
Khi m=5 thì pt sẽ là x^2+10x+25=0
=>x=-5
b: Thay x=-2 vào pt, ta được:
4-4m+m^2=0
=>m=2

a: Khi m=1 thì phương trình sẽ là \(x^2-3x-5=0\)
\(\text{Δ}=\left(-3\right)^2-4\cdot1\cdot\left(-5\right)=9+20=29\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{3-\sqrt{29}}{2}\\x_2=\dfrac{3+\sqrt{29}}{2}\end{matrix}\right.\)
b: \(\text{Δ}=\left(2m+1\right)^2-4\left(-m-4\right)\)
\(=4m^2+4m+1+4m+16\)
\(=4m^2+8m+17\)
\(=4m^2+4m+4+13\)
\(=\left(2m+2\right)^2+13>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
a, Thay m =1 ta đc
\(x^2-3x-5=0\)
\(\Delta=9-4\left(-5\right)=9+20=29>0\)
Vậy pt luôn có 2 nghiệm pb
\(x=\dfrac{3\pm\sqrt{29}}{2}\)
b, Ta có \(\Delta=\left(2m+1\right)^2-4\left(-m-4\right)=4m^2+4m+1+4m+16\)
\(=4m^2+8m+16+1=4\left(m^2+2m+4\right)+1=4\left(m+1\right)^2+13>0\)
vậy pt luôn có 2 nghiệm pb

a) x4 + (1 - 2m)x2 + m2 - 1 = 0 (1)
Đặt t=x2 ta dc PT: t2+(1-2m)t+m2-1=0(2)
Để PT (1) thì PT(2) vô nghiệm:
Để PT(2) vô nghiệm thì: \(\Delta=\left(1-2m\right)^2-4.\left(m^2-1\right)<0\Leftrightarrow1-4m+4m^2-4m^2+4<0\)
<=>5-4m<0
<=>m>5/4
b)Để PT(1) có 2 nghiệm phân biệt thì PT(2) có duy nhất 1 nghiệm
Để PT(2) có duy nhất 1 nghiệm thì:
\(\Delta=5-4m=0\Leftrightarrow m=\frac{5}{4}\)
c)Để PT(1) có 4 nghiệm phân biệt thì PT(2) có 2 nghiệm phân biệt:
Để PT(2) có 2 nghiệm phân biệt thì:
\(\Delta=5-4m\ge0\Leftrightarrow m\le\frac{5}{4}\)
Mem đây ko rành lắm sai bỏ qua
Chọn B