Có bao nhiêu giá trị nguyên của m để đồ thị hàm số y = x 2 - x 2 + x - 1 2 cắt trục hoành tại đúng hai điểm phân biệt?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án là A
Phương trình hoành độ giao điểm của đồ thị hàm số đã cho và trục hoành:
![]()
![]()
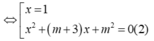
Đồ thị hàm số đã cho cắt trục hoành tại 3 điểm phân biệt ⇔ (1) có 3 nghiệm phân biệt ⇔ (2) có 2 nghiệm phân biệt khác 1
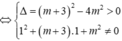
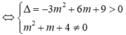
![]()
Do đó có 3 giá trị nguyên của m thỏa mãn ycbt.

Chọn đáp án A
Phương pháp
Nhẩm nghiệm của phương trình hoành độ giao điểm, từ đó tìm điều kiện để phương trình hoành độ giao điểm có 3 nghiệm phân biệt.

Để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt thì phương trình x 2 + ( m + 3 ) x + m 2 = 0 phải có hai nghiệm phân biệt khác 1
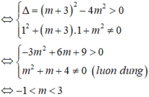
Do đó với -1<m<3 thì đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt
![]()

Đáp án D.
Phương trình hoành độ giao điểm của (C) và Ox là x 3 + a + 10 x 2 − x + 1 = 0 (*).
Dễ thấy x = 0 không là nghiệm của phương trình (*). Khi đó (*) ⇔ − a − 10 = x 3 − x + 1 x 2 .
Xét hàm số f x = x 3 − x + 1 x 2 = x − 1 x + 1 x 2 , có f ' x = x 3 + − 2 x 3 = 0 ⇔ x = 1.
Tính:
lim x → − ∞ x = − ∞ ; lim x → + ∞ x = + ∞ ; lim x → 0 − x = + ∞ ; lim x → 0 + x = − ∞ ; f 1 = 1.
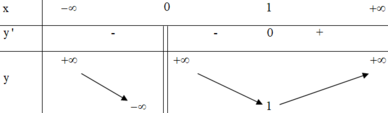
Dựa vào bảng biến thiên, ta thấy f x = − a − 10 có nghiệm duy nhất ⇔ a > − 11.
Kết hợp với a là số nguyên âm ⇒ Có 10 giá trị cần tìm.

Pt hoành độ giao điểm:
\(\sqrt{2x^2-2x-m}-x-1=0\)
\(\Leftrightarrow\sqrt{2x^2-2x-m}=x+1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\2x^2-2x-m=x^2+2x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x^2-4x-1=m\left(1\right)\end{matrix}\right.\)
Bài toán thỏa mãn khi (1) có 2 nghiệm pb \(x\ge-1\)
Từ đồ thị hàm \(y=x^2-4x-1\) ta thấy \(-5< m\le4\)

a: Thay x=-2 và y=-2 vào (d1), ta đc:
-2(2m+1)+m-3=-2
=>-4m-2+m-3=-2
=>-3m-5=-2
=>-3m=3
=>m=-1
b: Tọa độ giao của (d2) với trục hoành là:
y=0 và (2a+1)x+4a-3=0
=>x=-4a+3/2a+1
Để x nguyên thì -4a-2+5 chia hết cho 2a+1
=>\(2a+1\in\left\{1;-1;5;-5\right\}\)
=>\(a\in\left\{0;-1;2;-3\right\}\)

Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 2
\(\Leftrightarrow\hept{\begin{cases}y=0\\x=2\end{cases}}\)
Với x = 2; y = 0 thay vào hàm số ta được
\(\left(m+3\right).2+2m=0\Leftrightarrow2m+2m+6=0\)
\(\Leftrightarrow4m=-6\)
\(\Leftrightarrow m=-1,5\)
Vậy m = -1,5 là giá trị cần tìm



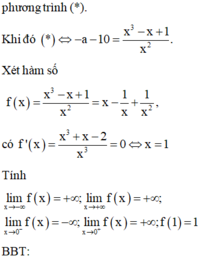

Chọn đáp án A.