Cho hàm số y = f(x) có đạo hàm f ' x = 1 2 x − 1 và f(1) = 1. Giá trị f(5) bằng:
A. 1 + ln 3.
B. ln 2
C. 1 + ln 2
D. ln 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,y'=8x^3-9x^2+10x\\ \Rightarrow y''=24x^2-18x+10\\ b,y'=\dfrac{2}{\left(3-x\right)^2}\\ \Rightarrow y''=\dfrac{4}{\left(3-x\right)^3}\)
\(c,y'=2cos2xcosx-sin2xsinx\\ \Rightarrow y''=-5sin\left(2x\right)cos\left(x\right)-4cos\left(2x\right)sin\left(x\right)\\ d,y'=-2e^{-2x+3}\\ \Rightarrow y''=4e^{-2x+3}\)

Bất phương trình m > f(x) - ln(-x) đúng với mọi x ∈ - 1 ; - 1 e
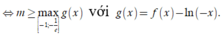
Ta có ![]()
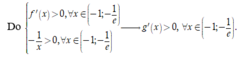
Suy ra hàm số g(x) đồng biến trên ![]()
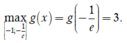
Chọn D.

Chọn A
Từ đồ thị của hàm số y = f'(x) ta có bảng biến thiên của hàm số y = f(x) trên đoạn [-1;2] như sau
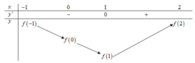
Nhận thấy
![]()
Để tìm ![]() ta so sánh f(-1) và f(2)
ta so sánh f(-1) và f(2)
Theo giả thiết, ![]()
![]()
Từ bảng biến thiên , ta có f(0) - f(1) > 0. Do đó f(2) - f(-1) > 0 ![]()
![]()
Đáp án A
∫ 1 5 f ' ( x ) d x = ∫ 1 5 1 2 x − 1 d x = 1 2 . ln 2 x − 1 5 1 = 1 2 ln 9 = f ( 5 ) − f ( 1 ) ⇒ f ( 5 ) = 1 2 ln 9 + 1 = ln 3 + 1