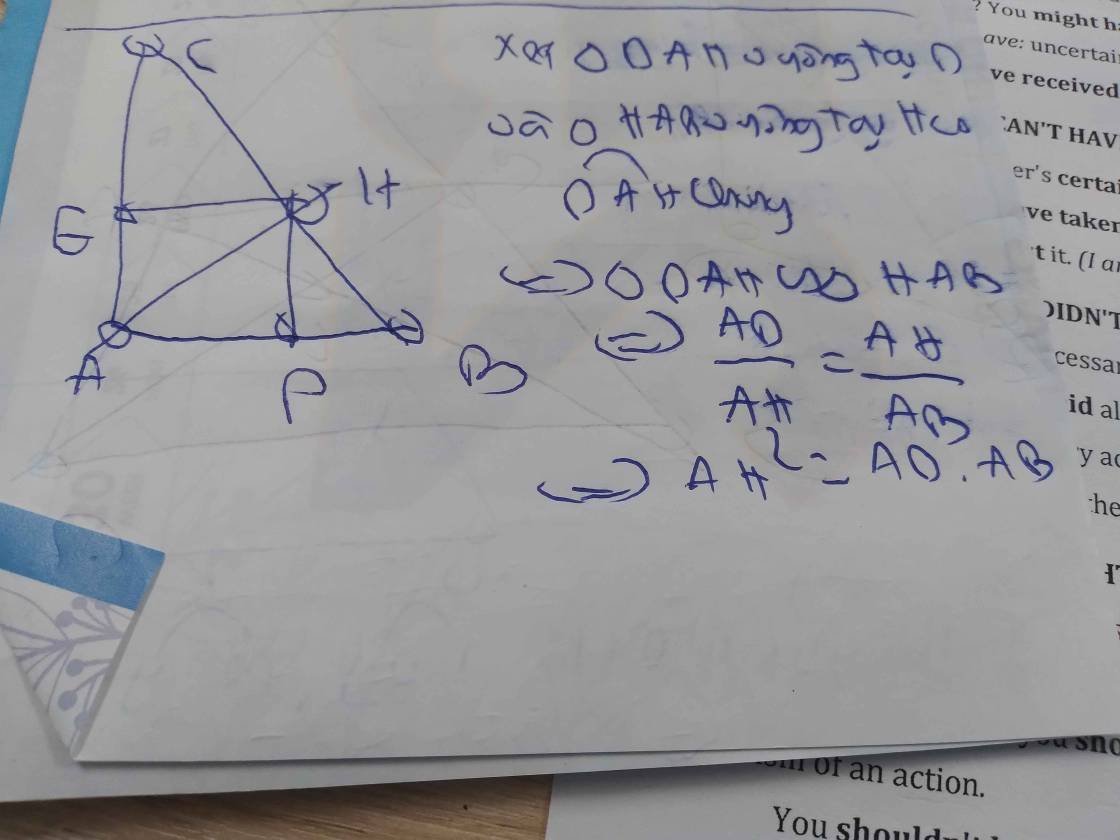
Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HE vuông góc với AB E thuộc AB; kẻ HF vuông góc với AC F thuộc AC a) Chứng minh: Tứ giác AEHF là hình chữ nhật. b) Gọi P là điểm đối xứng của H qua AB . Tứ giác APEF là hình gì? Vì sao? c) Đường thẳng đi qua C và song song với BP, cắt tia PA tại Q. Chứng minh: Q đối xứng với H qua F .