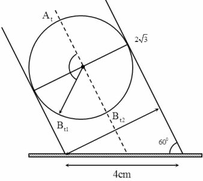
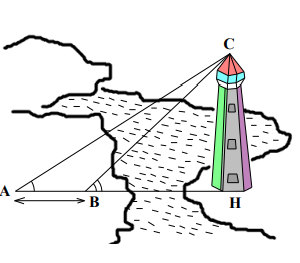
Tháp cột cờ quốc gia Lũng Cú thuộc huyện Đồng Văn tỉnh Hà Giang có đỉnh ở vị trí S, đáy thân tháp ở vị trí D. Hai vị trí A, B ở dưới thung lũng sao cho A, B, D, S cùng nằm trên một mặt phẳng và ở đó ta có thể quan sát được tháp đồng thời thực hiện đo đạc. H là hình chiếu vuông góc của S trên AB (hình vẽ).
Kết quả đo đạc như sau: AB = 15m, DAH ^ = 24 , 75 o , SAH ^ = 28 . 5 o , SBH ^ = 30 o .
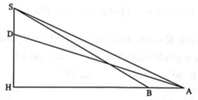
Chiều cao tháp cột cờ sấp sỉ bằng
A. 20,6 m.
B. 18,3 m.
C. 26,2 m.
D. 15,5 m.

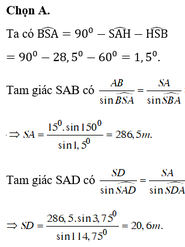
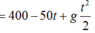


 Hình
Hình