Có bao nhiêu mặt cầu tiếp xúc với cả 3 mặt phẳng tọa độ mà tâm của các mặt cầu đó đều thuộc mặt phẳng (P): y – z + 2 = 0?
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án D
Giả sử mặt cầu (S) có tâm I a ; b ; c ∈ T : a + b + c = 0
Theo bài ra d I ; P = d I ; Q = d I ; R
⇔ 2 a − b − c − 2 6 = a − 2 b + c + 2 6 = a + b − 2 c + 2 6
⇒ 3 a − 2 = 3 b − 2 3 a − 2 = 3 c − 2 a + b + c = 0 ⇒ a = b 3 a + 3 b = 4 a = c 3 a + 3 c = 4
M N // B A '
TH1: a + b + c = 0 a = b a = c ⇒ I 0 ; 0 ; 0
Tương tự cho các trường hợp còn lại

Chọn A
Mặt phẳng (P) chứa đường tròn (C) (giao của 2 mặt cầu đã cho) có phương trình là: 6x + 3y + 2z = 0
Mặt phẳng (P) có phương trình là:
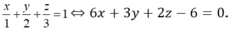
Do đó (P) // (ABC). Mặt cầu (S) tiếp xúc với cả ba đường thẳng AB, BC, CA sẽ giao với mặt phẳng (ABC) theo một đường tròn tiếp xúc với ba đường thẳng AB, BC, CA.
Trên mặt phẳng (ABC) có 4 đường tròn tiếp xúc với ba đường thẳng AB, BC, CA đó là đường tròn nội tiếp tam giác ABC và ba đường tròn bàng tiếp các góc A, B, C. Do đó có 4 mặt cầu có tâm nằm trên (P) và tiếp xúc với cả ba đường thẳng AB, BC, CA. Tâm của 4 mặt cầu là hình chiếu của tâm 4 đường tròn tiếp xúc với ba đường thẳng AB, BC, CA lên mặt phẳng (P).

Đáp án A
Phương pháp giải:
Xét vị trí tương đối của mặt phẳng, gọi phương trình tổng quát của mặt phẳng và tính toán dựa vào điều kiện tiếp xúc
Lời giải:
Gọi phương trình mặt phẳng cần tìm là (P): ax+by+cz+d=0
![]()
suy ra mp(P)//BC hoặc đi qua trung điểm của BC.
Mà B C → = ( - 4 ; 0 ; 0 ) và mp vuông góc với mp (Oyz) => (P) //BC
Với (P) //BC => a = 0 => by+cz+d=0



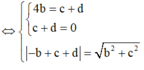

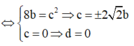
suy ra có ba mặt phẳng thỏa mãn