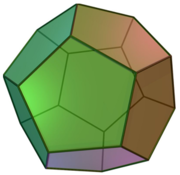
Cho hình thập nhị diện đều (tham khảo hình vẽ bên). Côsin của góc tạo bởi hai mặt phẳng có chung một cạnh của thập nhị diện đều bằng
A. 5 - 1 2
B. 5 - 1 4
C. 1 5
D. 1 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

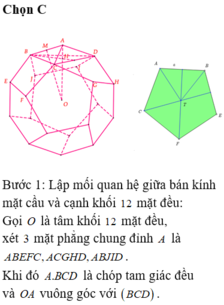
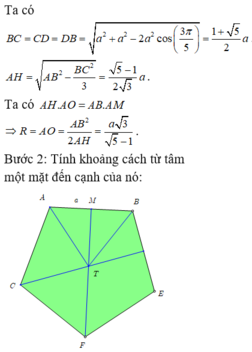
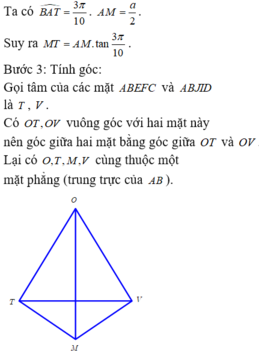
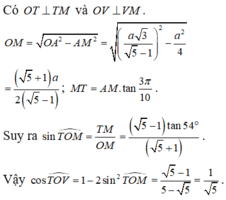

Đáp án B
Gọi O,M lần lượt là trọng tâm tam giác BCD, trung điểm cạnh CD. Khi đó
![]()
Do đó
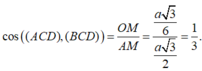

Đáp án B
Gọi L là điểm thỏa mãn A P ¯ = 3 P L ¯ và Q là trung điểm B ' C ' thì cosin cần tìm là
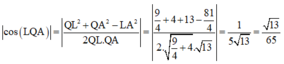

Dùng phương pháp tọa độ hóa.
Đặt hệ trục tọa độ, ở đây như thầy đã trình bày ta nên chọn gốc tại P trục Ox, Oy là PA và PC.
Gọi α góc tạo bởi hai mặt phẳng ( AB'C' ) và (MNP)
Khi đó cos α = n 1 → . n 2 → n 1 → . n 2 → = 13 65
Đáp án cần chọn là B

tham khảo
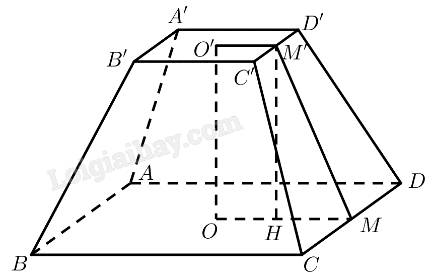
Mô hình hoá chân cột bằng gang bằng cụt chóp tứ giác đều \(ABCD.A'B'C'D'\) với \(O,O'\) là tâm của hai đáy.Vậy \(AB=2a,A'B'=a,OO'=2a\)
a)Gọi \(M,M'\) lần lượt là trung điểm của \(CD,C'D'.\)
\(A'B'C'D'\) là hình vuông \(\Rightarrow O'M\perp C'D\)
\(CDD'C\) là hình thang cân \(\Rightarrow MM'\perp C'D'\)
Vậy \(\widehat{MM'O}\) là góc phẳng nhị diện giữa mặt bên và đáy nhỏ,\(\widehat{M'MO}\) là góc phẳng nhị diện giữa mặt bên và đáy lớn.
Kẻ \(M'H\perp OM\left(H\in OM\right)\)
\(OMM'O'\) là hình chữ nhật
\(\Rightarrow OH=O'M'=\dfrac{a}{2},OM=a,MH=OM-OH=\dfrac{a}{2}\tan\widehat{M'MO}=\dfrac{M'H}{MH}=4\)
\(\Rightarrow\widehat{M'MO}=75,96^o\Rightarrow\widehat{MM'O'}=180^o-\widehat{M'MO}\\ =104,04^o\)
b)Diện tích đáy lớn là:\(S=AB^2=4a^{^2}\)
Diện tích đáy bé là:\(S'=A'B'^2=a^2\)
Thể tích hình chóp cụt là:
\(V_1=\dfrac{1}{3}h\left(S+\sqrt{SS'}+S'\right)\\ =\dfrac{1}{3}.2a\left(4a^2+\sqrt{4a^2.a^2}+a^2\right)=\dfrac{14a^3}{3}\)
Thể tích hình trụ rỗng là:\(V_2=\pi R^2h=\pi\left(\dfrac{a}{2}\right)^2.2a=\dfrac{\pi a^3}{2}\)
Thể tích chân cột là:\(V=V_1-V_2=\left(\dfrac{14}{3}-\dfrac{\pi}{2}\right)a^3\)