Cho hai số thực dương x, y thoả mãn 3sinx+ 15 sin x sin y +5 siny=7 sin( x+y) và x + y < π . Giá trị nhỏ nhất của x+y bằng
A. 2 π 3
B. π 6
C. 5 π 6
D. π 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

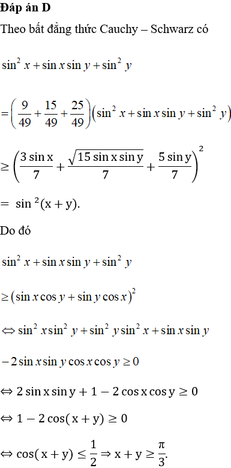

\(x+y+2xy=\dfrac{15}{2}\)\(\Rightarrow\dfrac{15}{2}\le\left(x+y\right)+\dfrac{\left(x+y\right)^2}{2}\)
\(\Leftrightarrow\left(x+y\right)^2+2\left(x+y\right)-15\ge0\)
\(\Leftrightarrow\left(x+y+5\right)\left(x+y-3\right)\ge0\)
\(\Leftrightarrow x+y\ge3\) (vì \(x+y+5>0\) với mọi x,y dương)
\(\Rightarrow P_{min}=3\)
Dấu = xảy ra <=> \(x=y=\dfrac{3}{2}\)

Theo bđt cauchy schwarz dang engel
\(\dfrac{1}{x}+\dfrac{1}{y}\ge\dfrac{4}{x+y}=\dfrac{4}{10}=\dfrac{2}{5}\)
Dấu ''='' xảy ra khi \(x=y=5\)
Vậy ...

\(\dfrac{1}{x}+\dfrac{2}{y}\le1\Rightarrow\dfrac{2}{y}\le1-\dfrac{1}{x}\Rightarrow y\ge\dfrac{2x}{x-1}=2+\dfrac{2}{x-1}\)
\(x+\dfrac{2}{z}\le3\Rightarrow x< 3;\dfrac{2}{z}\le3-x\Rightarrow z\ge\dfrac{2}{3-x}\Rightarrow y+z\ge2+\dfrac{2}{x-1}+\dfrac{2}{3-x}\)
Lúc này ta sẽ áp dụng bất đẳng thức Bunhiacopski
Ta có:
\(6^2\le\left(y+z\right)^2=\left(\sqrt{2}\dfrac{y}{\sqrt{2}}Z\right)^2\le3\left(\dfrac{y^2}{2}+z^2\right)=\dfrac{3}{2}\left(y^2+2z^2\right)\)
\(\Rightarrow P\ge24\). Dấu đẳng thức xảy ra khi và chỉ khi \(y=4,z=2\)
Vậy giá trị nhỏ nhật của P là 24