Cho hàm số y = f x có bảng xét dấu của f ' x
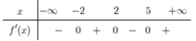
Hỏi hàm số g x = f 1 - x + x 3 3 - x 2 - 3 x đạt cực tiểu tại điểm nào dưới đây?
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

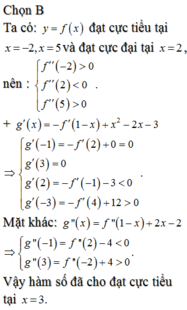

Đáp án B
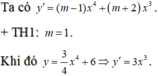
Suy ra hàm số đạt cực tiểu tại x=0 (loại).
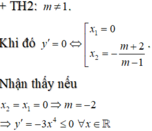
Hàm số luôn nghịch biến trên ℝ nên hàm số không có cực trị ( loại)
Vì vậy yêu cầu bài toán tương đương với
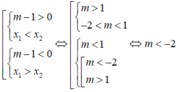
Suy ra số giá trị m nguyên thuộc khoảng (-2019;2019) là 2016.

Đáp án A
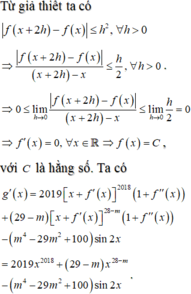
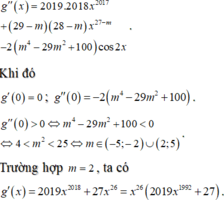
Vì x=0 là nghiệm bội chẵn của phương trình g'(x) = 0 nên trường hợp này loại
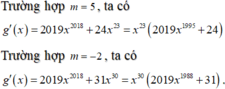
Vì x=0 là nghiệm bội chẵn của phương trình g'(x)= 0 nên trường hợp này loại.
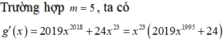
Dễ thấy g'(x) đổi dấu từ âm sang dương khi qua x=0 nên hàm số g(x) đạt cực tiểu tại x=0
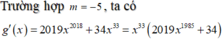
Dễ thấy g'(x) đổi dấu từ âm sang dương khi qua x=0 nên hàm số g(x) đạt cực tiểu tại x=0
Vậy m ∈ S = - 5 ; - 4 ; - 3 ; 3 ; 4 ; 5 nên tổng các bình phương của các phần tử của S là 100

Dựa vào bảng xét dấu của f '(x) ta có bảng biến thiên của hàm số trên đoạn [0;5] như sau
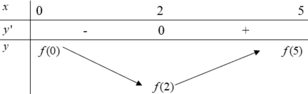
Suy ra ![]() Và
Và ![]()
Ta có ![]()
![]()
Vì f(x) đồng biến trên đoạn [2;5] nên ![]()
⇒ f(5)>f(0)
Vậy
![]()
Chọn đáp án D.

Nhận thấy y' đổi dấu khi qua x = -3 và x = 2 nên hàm số có 2 điểm cực trị. ( x = 1 không phải là điểm cực trị vì y' không đổi dấu khi qua x = 1). Chọn C.