Cho tập hợp . Có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số khác nhau lấy từ tập hợp S?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: A
S chỉ có 1 tập con
⇔ S = ∅ ⇔ (m - 1; m + 1) ⊂ (-∞; 1].
⇔ m + 1 ≤ 1 ⇔ m ≤ 0

Để \(x=\frac{a-20}{-3}\) ( a ∈ N* ) nhận giá trị dương
=> a - 20 nhận giá trị âm
=> a nhỏ hơn 20
a) S = { a ∈ N* | a < 20 }
\(S=\left\{...;17;18;19\right\}\)
b) ( Không hiểu đề , thông cảm , bạn làm nốt nhé ! )

Chọn A
Cách 1.
Giả sử ![]() Đặt
Đặt ![]() Khi đó
C
1
,
C
2
, C là ba tập con không giao nhau của S và S =
C
1
∪
C
2
∪
C
Khi đó
C
1
,
C
2
, C là ba tập con không giao nhau của S và S =
C
1
∪
C
2
∪
C
Khi đó mỗi phần tử x ∈ S có 3 khả năng: Hoặc thuộc tập C 1 hoặc thuộc tập C 2 hoặc thuộc tập C.
Do đó 12 phần tử sẽ có 3 12 cách chọn.
Trong các cách chọn nói trên có 1 trường hợp C 1 = C 2 = ∅ , C = S
Các trường hợp còn lại thì lặp lại 2 lần (đổi vai trò C 1 và C 2 cho nhau).
Do đó số cách chia là 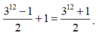
Cách 2.
Đặt S = S 1 ∪ S 2
Nếu
S
1
có k phần tử ![]()
![]()
![]()
![]()
Vậy số cách chọn 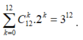
Nhưng trường hợp ![]() giống nhau và không hoán vị nên có
giống nhau và không hoán vị nên có  cách
cách

Tập hợp S có số phần tử là:
(166-6) : 4=40 (phần tử)
Cách làm đơn giản thế này thôi bạn nhé! Chúc bạn học tốt.
Chọn đáp án A.
Cách 1: Lấy 4 chữ số khác nhau từ tập S rồi sắp xếp theo một thứ tự nào đó ta được một số tự nhiên.
Vậy số tự nhiên gồm 4 chữ số khác nhau lấy từ tập hợp S là một chỉnh hợp chập 4 của S.
Do đó số các số tự nhiên gồm 4 chữ số khác nhau lấy từ tập hợp S là A 6 4 = 360 (số).
Cách 2: Có 6 cách chọn chữ số hàng nghìn.
Khi đó có 5 cách chọn chữ số hàng trăm.
Khi đã chọn xong chữ số hàng nghìn và chữ số hàng tram thì có 44 cách chọn chữ số hàng chục
Cuốin ùng, khi đã chọn xong chữ số hang nghìn, hằng trăm, hàng chục thì còn 3 cách chọn chữ số hàng đơn vị.
Vậy các số tự nhiên gồm 4 chữ số khác nhau lấy từ tập hợp S là 6.5.4.3 = 360 (số).