Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Tính theo a khoảng cách từ điểm G đến mặt phẳng (SCD)
A. a 6 9
B. a 6 3
C. 2 a 6 9
D. a 6 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Gọi O là tâm hình vuông ABCD và M là trung điểm CD có S O = a 2 2 và H là hình chiếu vuông góc của G lên mặt phẳng (ABCD).
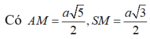
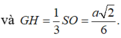
Vì
![]()
![]()
![]()
Và
![]()
![]()
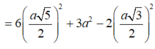
![]()
Vì vậy
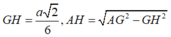
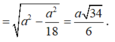
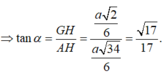

Đáp án là C.
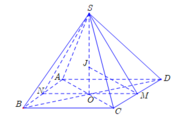
Gọi O là tâm hình vuông ABCD .Ta có đường cao của hình chóp SABCD là SO
V S A B C D = 1 3 S 0 . S A B C D ⇔ 3 6 a 8 = 1 3 S O . a 2 ⇒ S O = 3 2 a .
Xét tam giác SMO ta có SM= S 0 2 + O M 2 = ( 3 2 a ) 2 + ( a 2 ) 2 = a
Gọi M,N lần lượt là trung điểm của AB,CD.Khi đó J là tâm đường tròn nội tiếp tam giác SMN. Khi đó ta có MJ là đường phân giác của tam giác SMN.
Suy ra : S J J O = M S M O = a a = 2 ⇒ S J = 2 J O .
Mà S 0 = S J + J O = 3 2 a ⇔ 3 J O = 3 2 a ⇔ J O = 3 6
Chọn C