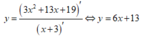Cho hàm số y = f x có bảng biến thiên như sau
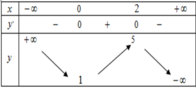
Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số có phương trình là
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án C
Từ bảng biến thiên ta thấy f x ≥ 1 > 0 , ∀ x > − 1 nên phương trình f(x) = 0 có một nghiệm duy nhất x 0 < − 1
Mặt khác ta có y = f x = f x , f x ≥ 0 f x , f x < 0
Do đó ta có bảng biến thiên của y= f x
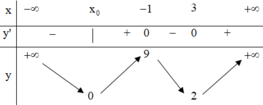
Từ bảng biến thiên ta thấy đồ thị hàm số y= f x có 3 điểm cực trị

Đáp án D
Ta vẽ lại bảng biến thiên của f x .

Từ bảng biến thiên này hàm số y = f x có cực trị

Chọn B.
Số điểm cực trị của đồ thị hàm số y=|f(x)| bằng số điểm cực trị của đồ thị hàm số y=f(x) cộng với số giao điểm của đồ thị hàm số y=f(x) với trục hoành (không tính điểm cực trị)
Vì đồ thị hàm số y=f(x) có 2 điểm cực trị và cắt trục Ox tại 1 điểm trên đồ thị hàm số y=|f(x)| có 2 + 1 = 3 điểm cực trị

Chọn B.
Cách 1: Số điểm cực trị của đồ thị hàm số y=|f(x)| bằng số điểm cực trị của đồ thị hàm số y=f(x) cộng với số giao điểm của đồ thị hàm số y=f(x)với trục hoành (không tính điểm cực trị)
Vì đồ thị hàm số y=f(x) có 2 điểm cực trị và cắt trục Ox tại 1 điểm nên đồ thị hàm số y=|f(x)| có 2 + 1 = 3 điểm cực trị

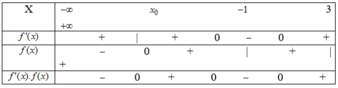
Đáp án: 3 cực trị

Chọn C
![]()
Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là y =6x +13 .
Phương pháp trắc nghiệm:
Tại điểm cực trị của đồ thị hàm số phân thức ,
ta có: f ( x ) g ( x ) = f ' ( x ) g ' ( x )
Vậy phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là