Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của thế năng đàn hồi W đ h của một con lắc lò xo vào thời gian t. Khối lượng vật nặng là 400 g. Lấy π 2 = 10. Biên độ dao động là
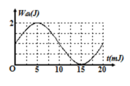
A. 2,5 cm
B. 1 cm.
C. 4 cm
D. 2 cm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
*Dựa vào đồ thị ta có thế năng đàn hồi cực đại đến thời điểm gần nhất thế năng đàn hồi cực tiểu tương ứng là
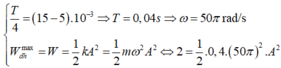
![]()

Đáp án C
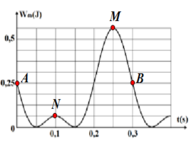
Từ đồ thị ta thấy :
+ Thế năng đàn hồi lớn nhất là 0,5625 J ứng với vị trí lò xo giãn nhiều nhất (biên dưới) – điểm M trên đồ thị
+ Thế năng đàn hồi ở biên trên ứng với vị trí lò xo bị nén cực đại – điểm N trên đồ thị.
Dễ thấy điểm N ứng với thế năng đàn hồi 0,0625 J
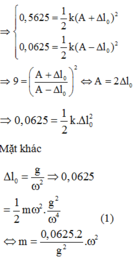
Để ý thấy từ điểm A đến điểm B thì đồ thị lặp lại, tức là bằng 1 chu kỳ
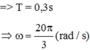
Thay vào (1) tìm được m ≈ 0 , 56 k g

Đáp án C

Mốc tính thế năng đàn hồi được chọn tại vị trí lò xo không biến dạng.
Từ đồ thị ta thấy mỗi ô có thế năng là 0 , 25 4 = 0 , 0625
Thế năng đàn hồi tại vị trí cao nhất: 0 , 0625 = 1 2 k A − Δ l 0 2 ( 1 )
Thế năng đàn hồi cực đại tại vị trí thấp nhất: W d max = 0 , 5625 = 1 2 k A + Δ l 0 2 ( 2 )
Lấy (2) chia (1): 9 = A + Δ l 0 2 A − Δ l 0 2 ⇒ 3 = A + Δ l 0 A − Δ l 0 ⇒ A = 2 Δ l 0 ( 3 )
Từ đồ thị ta thấy chu kì dao động của con lắc là: T = 0 , 3 s
Mặt khác con lắc lò xo treo có chu kì:
T = 2 π m k = 2 π Δ l 0 g ⇒ Δ l 0 = T 2 g 4 π 2 = 0 , 3 2 π 2 4 π 2 = 0 , 0225 m = 2 , 25 c m
⇒ A = 2 Δ l 0 = 4 , 5 c m Thế vào (1): k = 2.0 , 0625 A − Δ l 0 2 = 2.0 , 0625 0 , 045 − 0 , 0225 2 = 247 N / m
⇒ m = T 2 k 4 π 2 = 0 , 3 2 .247 4 π 2 = 0 , 56 k g
Chú ý: Gốc thế năng đàn hồi được chọn tại vị trí lò xo không dãn.

Đáp án B
Từ đồ thị ta thấy chu kỳ dao động của thế năng đàn hồi là 10.2ms = 20 ms. Suy ra chu kì dao động của con lắc lò xo là T = 2.20s = 40ms = 0,04 s
⇒ f = 1 T = 25 H z