Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng có phương trình P : x − y + 4 z − 2 = 0 và Q : 2 x − 2 z + 7 = 0 . Góc giữa hai mặt phẳng (P) và (Q) là
A. 90 0
B. 45 0
C. 60 0
D. 30 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Gọi I là tâm mặt cầu (S). Khi đó I (t; 1+t; 2+t) và ta có:
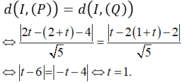
Vậy mặt cầu (S) có tâm I (1;2;3) và bán kính 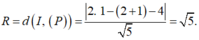
Do đó mặt cầu (S) có phương trình: ![]()

Đáp án D
Phương pháp giải:
Ứng dụng tích có hướng để tìm vectơ chỉ phương của đường thẳng giao tuyến và giải hệ phương trình để tìm tọa độ giao điểm của hai mặt phẳng
Lời giải: Ta có
![]()
Gọi d là giao tuyến của (P) và (Q).
Ta có
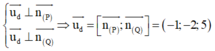
Xét hệ
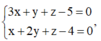
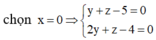
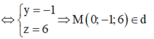
Vậy phương trình đường thẳng cần tìm là
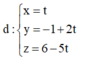
Đáp án C
Mặt phẳng (P) có vectơ pháp tuyến là n P → = 1 ; − 1 ; 4 . Mặt phẳng (Q) có vectơ pháp tuyến là n Q → = 2 ; 0 ; − 2 .
Cách 1: Tư duy tự luận
Góc giữa hai mặt phẳng (P) và (Q) được tính theo công thức:
cos P , Q ^ = cos n P → , n Q → = n P → . n Q → n P → . n Q → = 1.2 + − 1 .0 + 4. − 2 1 2 + − 1 2 + 4 2 . 2 2 + 0 2 + − 2 2
⇔ cos P , Q ^ = 1 2 . Vậy P , Q ^ = 60 0 .
Cách 2: Sử dụng máy tính cầm tay
Nhập vào máy tính các vectơ: VctA = 1 ; − 2 ; 4 , VctB = 2 ; 0 ; − 2 .