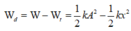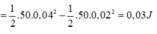Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
+ Chu kì dao động của con lắc lò xo
T = 2 π Δ l 0 g = 2 π 0 , 02 10 = 0 , 28 s
Chọn B.
Tại vị trí cân bằng lò xo biến dạng một đoạn 2cm ⇒ Δ l 0 = 2 c m .
Đáp án A
Lực đàn hồi đổi chiều tại vị trí lò xo không biến dạng.
Lực hồi phục (kéo về) đổi chiều tại vị trí cân bằng
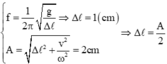
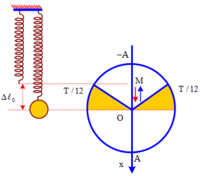
Thời gian mà lực đàn hồi ngược chiều lực hồi phục khi vật đi từ O đến M (M là vị trí lò xo không biến dạng) và ngược lại
Chọn đáp án A
? Lời giải:
+ Lực đàn hồi đổi chiều tại vị trí lò xo không biến dạng.
+ Lực hồi phục (kéo về) đổi chiều tại vị trí cân bằng
+ Thời gian mà lực đàn hồi ngược chiều lực hồi phục khi vật đi từ O đến M (M là vị trí lò xo không biến dạng) và ngược lại
Chọn đáp án A
? Lời giải:
+ Lực đàn hồi đổi chiều tại vị trí lò xo không biến dạng.
+ Lực hồi phục (kéo về) đổi chiều tại vị trí cân bằng
f = 1 2 π g Δ l ⇒ Δ l = 1 c m A = Δ l 2 + v 2 ω 2 = 2 c m ⇒ Δ l = A 2
+ Thời gian mà lực đàn hồi ngược chiều lực hồi phục khi vật đi từ O đến M (M là vị trí lò xo không biến dạng) và ngược lại
Δ t = 2. T 12 = T 6 = 1 30 s
Đáp án D
Phương pháp: Áp dụng định luật bảo toàn cơ năng
Cách giải:
Ở VTCB lò xo dãn một đoạn ∆ l
Vận tốc của vật bằng 0 ở biên, và lúc này lò xo không bị biến dạng nên A = 4cm
Ta có:
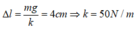
Động năng của vật ở cách VTCB 2cm là:
