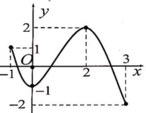
Cho đồ thị hàm số y=f(x) xác định, liên tục trên [-1;3] và có đồ thị như hình vẽ bên. Khẳng định nào sau đây sai?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
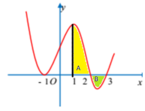
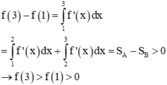
Đồ thị hàm số y = f(x) có dạng:
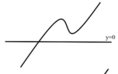
Đồ thị hàm số y = |f(x)| có dạng:
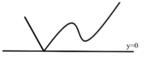
→ Hàm số y = |f(x)| có 3 điểm cực trị.

Chọn D
Trong khoảng ![]() đồ thị hàm số y= f’(x) nằm phía trên trục hoành nên hàm số y= f( x) đồng biến trên khoảng ( 0; π)
đồ thị hàm số y= f’(x) nằm phía trên trục hoành nên hàm số y= f( x) đồng biến trên khoảng ( 0; π)

Chọn D
Trong khoảng (0 ; + ∞) đồ thị hàm số y= f’( x) nằm phía dưới trục hoành- tức là f’( x)< 0 trên khoảng đó
=> Hàm số y= f(x) nghịch biến trên khoảng ![]()

Chọn C
Trong khoảng ( 0; 1) đồ thị hàm số y= f’( x) nằm phía dưới trục hoành nên trên khoảng này thì f’( x)< 0.
=> hàm số f(x) nghịch biến trên khoảng (0; 1) .

Chọn A.
Đồ thị hàm số có f’(x) có ba điểm tiếp xúc với trục hoành và không đổi dấu qua ba điểm đó. Vậy hàm số không có cực trị
Chọn D