Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Vì `VT=\sqrt{2x^2-9x+16}>0AAx`
`=>x-4>0`
`<=>x>4`
Bình phương 2 vế ta có:
`2x^2-9x+16=x^2-8x+16`
`<=>x^2-x=0`
`<=>x(x-1)=0`
Mà `x>4=>x-1>3>0`
`=>x(x-1)>0`
Vậy pt vô nghiệm
Ta có: x 2 + 4 x + 6 x 2 − 16 = 0
⇔ x 2 + 4 = 0 x + 6 = 0 x 2 − 16 = 0 ⇔ x 2 = − 4 < 0 V N x = 6 x = ± 4
Tổng các nghiệm của phương trình là: -6 + 4 + (-4) = -6
Đáp án cần chọn là D
Đáp án D
Phương trình tương đương với 4 4 x + 1 4 x = 4 ( m + 1 ) 2 x - 1 2 x + 16 - 8 m
⇔ 4 x + 1 4 x = ( m + 1 ) 2 x - 1 2 x + 4 - 2 m (1)
Đặt 2 x - 1 2 x = t → 4 x + 1 4 x = t 2 + 2 . Xét hàm số t ( x ) = 2 x - 1 2 x trên 0 ; 1 .
Đạo hàm t ' ( x ) = 2 x . ln 2 + ln 2 2 x > 0 , ∀ x ∈ 0 ; 1 ⇒ Hàm số t (x) luôn đồng biến trên [0;1]. Suy ra m i n x ∈ [ 0 ; 1 ] t ( x ) = t ( 0 ) = 0 và m a x x ∈ [ 0 ; 1 ] t ( x ) = t ( 1 ) = 3 2 . Như vậy t ∈ 0 ; 3 2 .
Phương trình (1) có dạng: t 2 + 2 = ( m + 1 ) t + 4 - 2 m ⇔ t 2 - ( m + 1 ) t + 2 m = 0
⇔ ( t - 2 ) t + 1 - m = 0 ⇔ t = 2 ∉ 0 ; 3 2 t = m - 1
Phương trình (1) có nghiệm x ∈ 0 ; 1 ⇔ phương trình ẩn t có nghiệm
t ∈ 0 ; 3 2 ⇔ 0 ≤ m - 1 ≤ 3 2 ⇔ 1 ≤ m ≤ 5 2 . Mà m ∈ ℤ nên m ∈ 1 ; 2 . Tổng tất cả các giá trị nguyên của m bằng 3.
ĐKXĐ: \(x>-1\)
Bước quan trọng nhất là tách hàm
\(\Leftrightarrow log_2\sqrt{x+3}-2\sqrt{x+3}+\left(x+3\right)=log_2\left(x+1\right)-2\left(x+1\right)+\left(x+1\right)^2\)
Đến đây coi như xong \(\Rightarrow\sqrt{x+3}=x+1\Rightarrow x=1\)
Đáp án D.
Phương trình tương đương với
Đặt 2 x - 1 2 x = t → 4 x + 1 4 x = t 2 + 2 . Xét hàm số t ( x ) = 2 x - 1 2 x trên 0 ; 1 .
Đạo hàm t ' ( x ) = 2 x . ln 2 + ln 2 2 x > 0 , ∀ x ∈ 0 ; 1 ⇒ Hàm số t ( x ) luôn đồng biến trên 0 ; 1 . Suy ra min x ∈ 0 ; 1 t ( x ) = t ( 0 ) = 0 và max x ∈ 0 ; 1 t ( x ) = t ( 1 ) = 3 2 . Như vậy t ∈ 0 ; 3 2 .
Phương trình (1) có dạng:
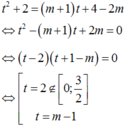
Phương trình (1) có nghiệm t ∈ 0 ; 1 ⇔ phương trình ẩn t có nghiệm t ∈ 0 ; 3 2 ⇔ 0 ≤ m - 1 ≤ 3 2 ⇔ 1 ≤ m ≤ 5 2 . Mà m ∈ ℤ nên m ∈ 1 ; 2 . Tổng tất cả các giá trị nguyên của m bằng 3.
\(\Leftrightarrow x^4-x^3+x^3-x^2-8x^2+8x+16x-16=0\\ \Leftrightarrow\left(x-1\right)\left(x^3+x^2-8x+16\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x^3+4x^2-3x^2-12x+4x+16\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+4\right)\left(x^2-3x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-4\\\left(x-\dfrac{3}{2}\right)^2+\dfrac{7}{4}=0\left(vô.n_o\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-4\end{matrix}\right.\)
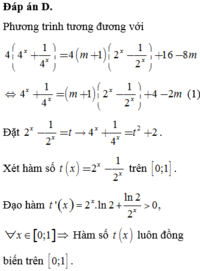
Đáp án B
Đặt a = 4 x − 16 , b = 16 x − 4 .
Ta có: P T ⇔ a 3 + b 3 = a + b 3 ⇔ 3 a b a 2 + b 2 = 0
⇔ a = 0 ∨ b = 0 ⇒ x = 2 ∨ x = 1 2
Vậy tổng tất cả các nghiệm thực của PT là 2 + 1 2 = 5 2 .