Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C
Gọi d là đường thẳng cần tìm.
Đường thẳng cần tìm qua A và nhận 
là véc tơ chỉ phương nên có phương trình:
Chọn B.
Vì đường tròn (C) cắt Δ tại hai điểm phân biệt A và B nên tọa độ điểm A và B là nghiệm của hệ phương trình:
Gọi H là trung điểm của AB suy ra IH ⊥ AB ⇒ IH ⊥ Δ.
Xét tam giác AIH vuông tại H ta có:
A H 2 + I H 2 = A I 2 ⇒ A H 2 = A I 2 - I H 2
Mặt phẳng (P) qua A và vuông góc d có phương trình:
\(2\left(x-1\right)+2\left(y+1\right)+1\left(z-1\right)=0\)
\(\Leftrightarrow2x+2y+z-1=0\)
Đường thẳng d' song song d và đi qua B (nên d' vuông góc (P)) có dạng:
\(\left\{{}\begin{matrix}x=4+2t\\y=2+2t\\z=-2+t\end{matrix}\right.\)
\(\Rightarrow\) Giao điểm C của d' và (P) thỏa mãn:
\(2\left(4+2t\right)+2\left(2+2t\right)-2+t-1=0\Rightarrow t=-1\Rightarrow C\left(2;0;-3\right)\)
\(\Rightarrow\overrightarrow{AC}=\left(1;1;-4\right)\Rightarrow\) là 1 vtcp của \(\Delta\Rightarrow\) D là đáp án đúng
Chọn D
Xét hàm số:
Do đó d (B; d) nhỏ nhất khi f(t) đạt giá trị nhỏ nhất bằng 27 tại t = 2/3. Suy ra 
. Chọn một vectơ chỉ phương của đường thẳng d là 
Vậy phương trình đường thẳng 
a. (P) vuông góc denta nên nhận (1;2;3) là 1 vtpt
Phương trình (P):
\(1\left(x-2\right)+2\left(y-1\right)+3\left(z-3\right)=0\)
\(\Leftrightarrow x+2y+3z-13=0\)
b. \(\overrightarrow{AB}=\left(1;2;-1\right)\) ; \(\overrightarrow{n_{\left(P\right)}}=\left(1;1;1\right)\)
\(\left[\overrightarrow{AB};\overrightarrow{n_{\left(P\right)}}\right]=\left(3;-2;-1\right)\)
Phương trình mp:
\(3\left(x-1\right)-2\left(y+1\right)-1\left(z-2\right)=0\)
\(\Leftrightarrow3x-2y-z-3=0\)
1: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a+b=-2\\2a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=1-2a=1-2\cdot\left(-3\right)=7\end{matrix}\right.\)
2: Vì (d)//y=-3x+2 nên a=-3
Vậy: y=-3x+b
Thay x=3 và y=3 vào y=-3x+b, ta được:
b-9=3
hay b=12
Đáp án C
Gọi H là hình chiếu vuông góc của điểm M trên đường thẳng Δ. Ta có:
H ∈ Δ => H(1 + t; 2 + t; 1 + 2t)
u Δ → = (1; 1; 2), MH → = (1- t; t + 1; 2t - 3)
MH ⊥ Δ <=> u Δ → . MH → = 0 <=> 1.(t - 1) + 1.(t + 1) + 2(2t - 3) = 0
<=> 6t - 6 = 0 <=> t = 1 => H(2; 3; 3)
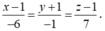
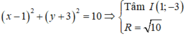
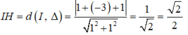
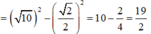
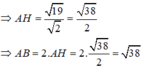
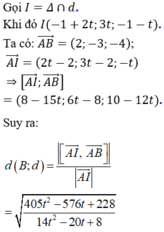
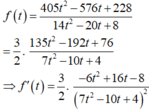
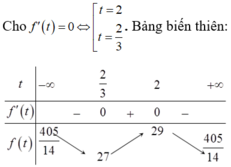
Đáp án là D.
Xét f t = 405 t 2 − 576 t + 228 14 t 2 − 20 t + 8 ⇒ f ' t = − 36 t 2 + 96 t − 48 14 t 2 − 20 t + 8 2
f ' t = 0 ⇔ t = 2 t = 2 3 . Vậy max f t = f 2 ⇒ t = 2
+ Đường thẳng d đi qua A 1 ; 2 ; − 1 và có VTCP A M → = 2 ; 4 ; − 2 = 2 1 ; 2 ; − 1