Rút gọn biểu thức 25 - (15 - x + 303) +303
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) 2x + (-61) - (21 - 61) = 2x - 21 + (61 - 61) = 2x - 21.
b) (- 3 - x + 5) + 3 = (- 3 + 3) + 5 - x = 5 - x.
c) 11- (13 - x) + (13 - 11) = (11- 11) + (13- 13) + x = x
d) 25 - ( 15 - x + 303) + 303 = 25 - 15 + (303 - 303) + x = x + 10



Không thể rút gọn được nha  I can rest your love on me
I can rest your love on me

1 Tìm số nguyên x bik:
a.-( 2x+2)+25=-19
-2x - 2 + 25 = - 19
-2x = -19+2-25
-2x = -42
x = 21
b.1-(12+3x)=7
1 - 12 - 3x = 7
- 11 - 3x = 7
-3x = 7 + 11
- 3x = 18
x = -6
c.-(2x+2)+25=-19
giống câu a nhé
2.Rút gọn biểu thức
a.2x+(-61)-(21-61)
= 2x - 61 - 21 + 61
= 2x - 21
b. (-3-x+5)+3
= 2 - x + 3
= -1 -x
c.11-(13-x)+(13-11)
= 11 - 13 + x + 13 - 11
= x
d.25-(15-x+303)+303
= 25 - 15 + x - 303 + 303
= 10 + x
e.x+(-81)-(11-8)
= x - 81 - 11 + 8
= x - 84
f. (-1-x+2)+1
= -1 - x + 2 + 1
= - x + 2
g.15-(11-x)+(11-15)
= 15 - 11 + x + 11 - 15
= x
i) 15-(15-x+202)+202
= 15 - 15 + x - 202 + 202
= x
3.Chứng minh đẳng thức
a.-(59-3x)+39=3x-20
- 59 + 3x + 39 = 3x - 20
- 59 + 39 + 20 = 3x - 3x
0 = 0
b.-(a+b+c)+(b-c)-(a-c-1)=1+c-29
b - a - b - c + b - c - a + c + 1 = 1 + c - 29
b - a - b - c + b - c - a + c - c = 1 - 29 - 1
- 2a + b - 2c = - 29
chịu luôn -__-
c.-(19-2x)+39=2x+20
- 19 + 2x + 39 = 2x + 20
2x - 2x = 20 + 19 - 29
0 = 0
d.-(a+b+c)+b-c-( a-c+1)=c-2a-1
- a - b - c + b - c - a + c - 1 = c - 2a - 1
- a - b - c + b - c - a + c + 2a - c = -1 + 1
- 2c = 0
c = 0
Vậy c = 0

\(log_{a^3}b.log_ba=\dfrac{1}{3}.log_ab.log_ba=\dfrac{1}{3}\)
\(log_{a^{10}}b^5.log_{b^3}a^9=\dfrac{1}{10}.5.log_ab.\dfrac{1}{3}.9.log_ba=\dfrac{3}{2}\)
\(log_{a^{107}}b^{101}.log_{b^{303}}a^{428}=\dfrac{1}{107}.101.log_ab.\dfrac{1}{303}.428.log_ba=\dfrac{4}{3}.log_ab.log_ba=\dfrac{4}{3}\)
a: \(log_{a^3}b\cdot log_ba=\dfrac{1}{3}\cdot log_ab\cdot log_ba=\dfrac{1}{3}\)
b: \(log_{a^{10}}b^5\cdot log_{b^3}a^9\)
\(=\dfrac{1}{10}\cdot log_ab^5\cdot\dfrac{1}{3}\cdot log_ba^9\)
\(=\dfrac{1}{30}\cdot5\cdot log_ab\cdot9\cdot log_ba=\dfrac{45}{30}=\dfrac{3}{2}\)
c: \(log_{a^{107}}b^{101}\cdot log_{b^{303}}a^{428}\)
\(=\dfrac{1}{107}\cdot log_ab^{101}\cdot\dfrac{1}{303}\cdot log_ba^{428}\)
\(=\dfrac{1}{107}\cdot101\cdot log_ab\cdot\dfrac{1}{303}\cdot428\cdot log_ba\)
\(=4\cdot\dfrac{1}{3}=\dfrac{4}{3}\)

C = (-15 + |x|) + (25 - |-x|)
= -15 + |x| + 25 - |-x|
= (25 - 15) + |x| - |-x|
= 10 + |x| - |-x|
Ta có: |x| = |-x| => |x| - |-x| = 0
=> C = 10 + |x|
C = (-15 + IxI ) + ( 25 - I-xI)
C = (-15 + x ) + ( 25 - x )
C = -15 + x + 25 - x
C = ( -15 + 25 ) + ( x - x )
C = 10 + 0
C = 10
Vậy C = 10

P = ( - 15 + | x | ) + ( 25 - | - x | )
P = ( - 15 + x ) + ( 25 - x )
P = - 15 + x + 25 - x
P = - 15 + 25 + x - x
P = 25 - 15 + 0
P = 10
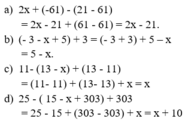
25 - ( 15 - x + 303) + 303 = 25 - 15 + (303 - 303) + x = x + 10